题目内容
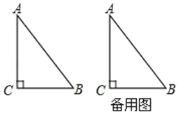
【题目】如图，已知在△ABC中，P为AB上一点，连接CP，以下条件中不能判定△ACP∽△ABC的是（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
A、加一公共角，根据两角对应相等的两个三角形相似可以得结论；
B、加一公共角，根据两角对应相等的两个三角形相似可以得结论；
C、其夹角不相等，所以不能判定相似；
D、其夹角是公共角，根据两边的比相等，且夹角相等，两三角形相似．
A、∵∠A=∠A，∠ACP=∠B，
∴△ACP∽△ABC，
所以此选项的条件可以判定△ACP∽△ABC；
B、∵∠A=∠A，∠APC=∠ACB，
∴△ACP∽△ABC，
所以此选项的条件可以判定△ACP∽△ABC；
C、∵
，
当∠ACP=∠B时，△ACP∽△ABC，
所以此选项的条件不能判定△ACP∽△ABC；
D、∵
，
又∠A=∠A，
∴△ACP∽△ABC，
所以此选项的条件可以判定△ACP∽△ABC，
本题选择不能判定△ACP∽△ABC的条件，
故选C．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
