题目内容
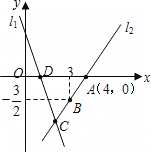
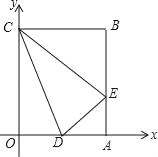
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,若BC=9,tan∠CDA=![]() ,求BE的长.
,求BE的长.

【答案】(1)证明见解析(2)![]()
【解析】分析: (1)连OD,OE,根据圆周角定理得到∠ADO+∠1=90°,而∠CDA=∠CBD,∠CBD=∠1,于是∠CDA+∠ADO=90°;
(2)根据切线的性质得到ED=EB,OE⊥BD,则∠ABD=∠OEB,得到tan∠CDA=tan∠OEB=![]() =
=![]() ,易证Rt△CDO∽Rt△CBE,得到
,易证Rt△CDO∽Rt△CBE,得到![]() =
=![]() =
=![]() =
=![]() ,求得CD,然后在Rt△CBE中,运用勾股定理可计算出BE的长.
,求得CD,然后在Rt△CBE中,运用勾股定理可计算出BE的长.
详解:
(1)证明:连OD,OE,如图,

∵AB为直径,
∴∠ADB=90°,即∠ADO+∠1=90°,
又∵∠CDA=∠CBD,
而∠CBD=∠1,
∴∠1=∠CDA,
∴∠CDA+∠ADO=90°,即∠CDO=90°,
∴CD是⊙O的切线;
(2)解:∵EB为⊙O的切线,ED是切线,
∴ED=EB,∵OB=OD,
∴OE⊥DB,
∴∠ABD+∠DBE=90°,∠OEB+∠DBE=90°,
∴∠ABD=∠OEB,
∴∠CDA=∠OEB.
而tan∠CDA=![]() ,
,
∴tan∠OEB=![]() =
=![]() ,
,
∵Rt△CDO∽Rt△CBE,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴CD=![]() ×9=6,
×9=6,
在Rt△CBE中,设BE=x,
∴(x+6)2=x2+92,
解得x=![]() .
.
即BE的长为![]() .
.
点睛: 本题考查了切线的判定与性质:过半径的外端点与半径垂直的直线是圆的切线;也考查了圆周角定理的推论以及三角形相似的判定与性质,熟练应用切线判定是解题的关键.

 名校课堂系列答案
名校课堂系列答案【题目】某市在城中村改造中,需要种植![]() 、
、![]() 两种不同的树苗共
两种不同的树苗共![]() 棵,经招标,承包商以
棵,经招标,承包商以![]() 万元的报价中标承包了这项工程,根据调查及相关资料表明,
万元的报价中标承包了这项工程,根据调查及相关资料表明, ![]() 、
、![]() 两种树苗的成本价及成活率如表:
两种树苗的成本价及成活率如表:
品种 | 购买价(元/棵) | 成活率 |
|
|
|
|
|
|
设种植![]() 种树苗
种树苗![]() 棵,承包商获得的利润为
棵,承包商获得的利润为![]() 元.
元.
(![]() )求
)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(![]() )政府要求栽植这批树苗的成活率不低于
)政府要求栽植这批树苗的成活率不低于![]()