题目内容
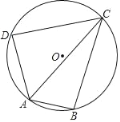
【题目】如图,矩形ABCD中,AD=5,AB=8,点E为DC上一个动点,把△ADE沿AE折叠,若点D的对应点D′,连接D′B,以下结论中:①D′B的最小值为3;②当DE=![]() 时,△ABD′是等腰三角形;③当DE=2是,△ABD′是直角三角形;④△ABD′不可能是等腰直角三角形;其中正确的有_____.(填上你认为正确结论的序号)
时,△ABD′是等腰三角形;③当DE=2是,△ABD′是直角三角形;④△ABD′不可能是等腰直角三角形;其中正确的有_____.(填上你认为正确结论的序号)
【答案】①②④
【解析】
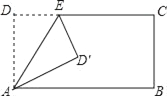
当D′落在线段AB上时,D′B的值最小,此时D′B=AB﹣AD=3,得出①正确;
过D′作MN⊥AB交AB于点N,交CD于点M,设AN=x,则EM=x﹣2.5,证出∠ED′M=∠D′AN,因此△EMD′∽△D′NA,得出对应边成比例![]() ,求出x=4,得出AN=BN,因此AD′=D′B,得出②正确;
,求出x=4,得出AN=BN,因此AD′=D′B,得出②正确;
当DE=2时,假设△ABD′是直角三角形,则E、D′、B在一条直线上,作EF⊥AB于点F,由勾股定理求出D′B、EB,得出③不正确;
当AD′=D′B时,由勾股定理的逆定理得出△ABD′不是直角三角形,当△ABD′是直角三角形时,由勾股定理求出D′B,得出AD′≠D′B,因此△ABD′不可能是等腰直角三角形,得出④正确.
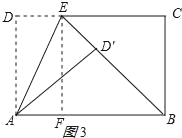
当D′落在线段AB上时,D′B的值最小,如图1所示:
此时D′B=AB﹣AD=8﹣5=3,
∴①正确;
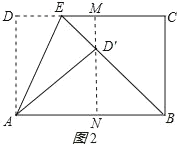
过D′作MN⊥AB交AB于点N,交CD于点M,如图2所示:
设AN=x,则EM=x﹣2.5,
∵∠AD′N=∠DAD′,∠ED′M=180°﹣∠AD′E﹣∠AD′N=180°﹣90°﹣∠AD′N=90°﹣∠AD′N,
∴∠ED′M=90°﹣∠DAD′,
∵∠D′AN=90°﹣∠DAD′,
∴∠ED′M=∠D′AN,
∵MN⊥AB,
∴∠EMD′=∠AND′,
∴△EMD′∽△D′NA,
∴![]() ,
,
即,![]()
解得:x=4,
∴AN=BN,
∴AD′=D′B,
即△ABD′是等腰三角形,
∴②正确;
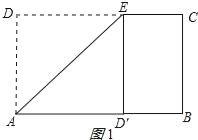
当DE=2时,假设△ABD′是直角三角形,
则E、D′、B在一条直线上,
作EF⊥AB于点F,如图3所示:
D′B=![]() =
=![]() ,EB=
,EB=![]() ,
,
∵![]() ≠
≠![]()
∴③不正确;
当AD′=D′B时,52+52≠82,
∴△ABD′不是直角三角形,
当△ABD′是直角三角形时,D′B=![]() =
=![]() ,
,
∴AD′≠D′B,
∴△ABD′不可能是等腰直角三角形,
∴④正确;
故答案为:①②④.