题目内容
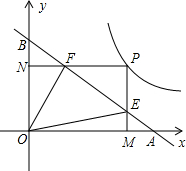 已知直线l与x轴、y轴分别交于A(2,0)、B(0,2)两点,双曲线y=
已知直线l与x轴、y轴分别交于A(2,0)、B(0,2)两点,双曲线y=| k |
| x |
(1)如果S△EOF=
| 5 |
| 6 |
| 3 |
| 2 |
(2)当P在(1)中双曲线上移动,∠EOF的大小始终为45°不变,此时,双曲线上存在这样的点P,使OE=OF,求出此时点P的坐标.
考点:反比例函数综合题
专题:综合题
分析:(1)先用待定系数法求出直线l的解析式,设出E点坐标,再根据S△EOF=S△AOF-S△AOE即可得出E点坐标,进而得出P点坐标,把P点坐标代入双曲线y=
即可得出结论;
(2)过点O作OD⊥AB于点D,因为OB=OA,故BD=AD,当OE=OF时可得DE=DF,故可得出BF=AE,再根据△BNF与△AME均是等腰直角三角形可知BN=NF=ME=AM,故ON=OM,即四边形NOMP是正方形,设P(x,x),代入(1)中反比例函数的解析式即可得出x的值,进而得出结论.
| k |
| x |
(2)过点O作OD⊥AB于点D,因为OB=OA,故BD=AD,当OE=OF时可得DE=DF,故可得出BF=AE,再根据△BNF与△AME均是等腰直角三角形可知BN=NF=ME=AM,故ON=OM,即四边形NOMP是正方形,设P(x,x),代入(1)中反比例函数的解析式即可得出x的值,进而得出结论.
解答:解:(1)设直线l的解析式为y=kx+b(k≠0),
∵A(2,0)、B(0,2),
∴
,解得
,
∴此直线的解析式为y=-x+2,
∵点E在直线l上,
∴设E(a,-a+2),
∵S△EOF=
,PM=
,PM⊥x轴于M,PN⊥y轴于N,
∴S△EOF=S△AOF-S△AOE=
OA•PM-
OA•ME
=
×2×
-
×2×(-a+2)
=
+a-2=
,
解得a=
,
∴E(
,
),
∴P(
,
),
∵点P在双曲线y=
上,
∴k=
×
=2,
∴抛物线的解析式为:y=
;
(2)如图所示,过点O作OD⊥AB于点D,
∵OB=OA,
∴BD=AD,
∴当OE=OF时DE=DF,
∴BF=AE,
∵△BNF与△AME均是等腰直角三角形,
∴BN=NF=ME=AM,
∴ON=OM,即四边形NOMP是正方形,
设P(x,x),则x=
,解得x=
或x=-
(舍去),
∴P(
,
).
∵A(2,0)、B(0,2),
∴
|
|
∴此直线的解析式为y=-x+2,
∵点E在直线l上,
∴设E(a,-a+2),
∵S△EOF=
| 5 |
| 6 |
| 3 |
| 2 |
∴S△EOF=S△AOF-S△AOE=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
=
| 3 |
| 2 |
| 5 |
| 6 |
解得a=
| 4 |
| 3 |
∴E(
| 4 |
| 3 |
| 2 |
| 3 |
∴P(
| 4 |
| 3 |
| 3 |
| 2 |
∵点P在双曲线y=
| k |
| x |
∴k=
| 4 |
| 3 |
| 3 |
| 2 |
∴抛物线的解析式为:y=
| 2 |
| x |
(2)如图所示,过点O作OD⊥AB于点D,
∵OB=OA,

∴BD=AD,
∴当OE=OF时DE=DF,
∴BF=AE,
∵△BNF与△AME均是等腰直角三角形,
∴BN=NF=ME=AM,
∴ON=OM,即四边形NOMP是正方形,
设P(x,x),则x=
| 2 |
| x |
| 2 |
| 2 |
∴P(
| 2 |
| 2 |
点评:本题考查的是反比例函数综合题,涉及到用待定系数法求一次函数及反比例函数的解析式、等腰三角形的性质等知识,难度适中.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
已知点P(-3,4),则点P到x轴的距离是( )
| A、-3 | B、-4 | C、3 | D、4 |
某班有49名学生,一天,该班一男生因事请假,当天的男生人数恰好为女生人数的一半.设该班有男生x人,女生y人,则可列方程组为( )
A、
| |||||||||
B、
| |||||||||
C、
| |||||||||
D、
|
如果一个多边形的内角和等于它的外角和,则这个多边形是( )边形.
| A、四 | B、五 | C、六 | D、七 |
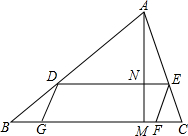 如图,△ABC有一个内接平行四边形DEFG,△ABC的高AM=80cm,底BC=120cm.
如图,△ABC有一个内接平行四边形DEFG,△ABC的高AM=80cm,底BC=120cm. 在弹性限度内,弹簧深长的长度与拉力成正比.如图小明手中拿着由三根相同的弹簧组成的弹簧拉力器.已知拉力器的长度y与拉力x是一次函数关系,y与x的部分对应值如下表.
在弹性限度内,弹簧深长的长度与拉力成正比.如图小明手中拿着由三根相同的弹簧组成的弹簧拉力器.已知拉力器的长度y与拉力x是一次函数关系,y与x的部分对应值如下表.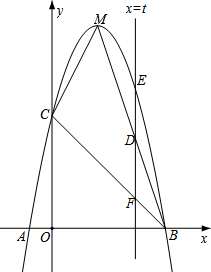 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,其中A点坐标为(-1,0),线段AB=6,
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,其中A点坐标为(-1,0),线段AB=6,