题目内容
【题目】阅读下面材料:

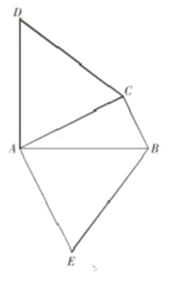
小亮遇到这样问题:如图1,已知AB∥CD,EOF是直线AB、CD间的一条折线.判断∠O、∠BEO、∠DFO三个角之间的数量关系.小亮通过思考发现:过点O作OP∥AB,通过构造内错角,可使问题得到解决.
请回答:∠O、∠BEO、∠DFO三个角之间的数量关系是 .
参考小亮思考问题的方法,解决问题:
(2)如图2,将△ABC沿BA方向平移到△DEF(B、D、E共线),∠B=50°,AC与DF相交于点G,GP、EP分别平分∠CGF、∠DEF相交于点P,求∠P的度数;
(3)如图3,直线m∥n,点B、F在直线m上,点E、C在直线n上,连接FE并延长至点A,连接BA、BC和CA,做∠CBF和∠CEF的平分线交于点M,若∠ADC=α,则∠M= (直接用含α的式子表示).
【答案】(1)∠EOF=∠BEO+∠DFO;(2)65°;(3)90°-![]() α.
α.
【解析】
(1)根据平行线的性质求出∠EOM=∠BEO,∠FOM=∠DFO,即可得出答案;
(2)由DF∥BC,AC∥EF,推出∠EDF=∠B=50°,∠F=∠CGF,推出∠DEF+∠F=180°-50°=130°,再由三角形内角和定理可得∠P+∠FGP=∠F+∠FEP,由此即可解决问题;
(3)由∠M=∠FBM+∠CEM=![]() ∠FBC+
∠FBC+![]() ∠CEM=
∠CEM=![]() (180°-α)=90°-
(180°-α)=90°-![]() α即可解决问题.
α即可解决问题.
(1)如图1中,

∵OP∥AB
∴∠EOP=∠BEO,
∵AB∥CD,
∴OP∥CD,
∴∠FOP=∠DFO,
∴∠EOP+∠FOP=∠BEO+∠DFO,
即:∠EOF=∠BEO+∠DFO;
故答案为:∠EOF=∠BEO+∠DFO.
(2)如图2中,
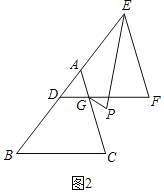
∵DF∥BC,AC∥EF,
∴∠EDF=∠B=50°,∠F=∠CGF,
∴∠DEF+∠F=180°-50°=130°,
∵∠P+∠FGP=∠F+∠FEP,
∴∠P=∠F+∠FEP-∠FGP=![]() ∠DEF+
∠DEF+![]() ∠F=65°.
∠F=65°.
(3)如图3中,
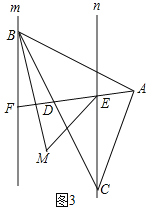
易知∠M=∠FBM+∠CEM,
∵BF∥EC,
∴∠DCE=∠DBF,
∵∠DEC+∠DCE=180°-α,
∠FBM+∠CEM=![]() ∠FBC+
∠FBC+![]() ∠CED=
∠CED=![]() (180°-α)=90°-
(180°-α)=90°-![]() α.
α.
故答案为90°-![]() α.
α.