题目内容
【题目】【阅读理解】
我们知道,1+2+3+…+n=![]() ,那么12+22+32+…+n2结果等于多少呢?
,那么12+22+32+…+n2结果等于多少呢?
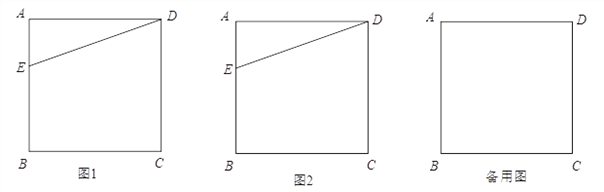
在图1所示三角形数阵中,第1行圆圈中的数为1,即12,第2行两个圆圈中数的和为2+2,即22,…;第n行n个圆圈中数的和为![]() ,即n2,这样,该三角形数阵中共有
,即n2,这样,该三角形数阵中共有![]() 个圆圈,所有圆圈中数的和为12+22+32+…+n2.
个圆圈,所有圆圈中数的和为12+22+32+…+n2.


【规律探究】
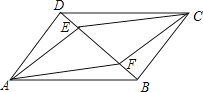
将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n﹣1行的第一个圆圈中的数分别为n﹣1,2,n),发现每个位置上三个圆圈中数的和均为 ,由此可得,这三个三角形数阵所有圆圈中数的总和为:3(12+22+32+…+n2)= ,因此,12+22+32+…+n2= .
【解决问题】
根据以上发现,计算: ![]() 的结果为 .
的结果为 .
【答案】【规律探究】2n+1, ![]() ,
, ![]() ;【解决问题】1345.
;【解决问题】1345.
【解析】试题分析:【规律探究】将同一位置圆圈中的数相加即可,所有圈中的数的和应等于同一位置圆圈中的数的和乘以圆圈个数,据此可得,每个三角形数阵和即为三个三角形数阵和的![]() ,从而得出答案;
,从而得出答案;
【解决问题】运用以上结论,将原式变形为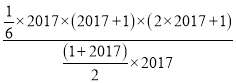 ,化简计算即可得.
,化简计算即可得.
试题解析:【规律探究】由题意知,每个位置上三个圆圈中数的和均为n﹣1+2+n=2n+1;
![]()
![]() =
=![]() ,
,
![]()
![]() ,
,
故答案为:2n+1, ![]() ,
, ![]() ;
;
【解决问题】![]()
=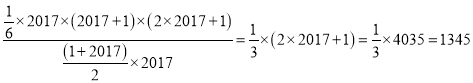 .
.

练习册系列答案
相关题目
【题目】在小方格纸上按下面的方式涂色:

① ② ③ ④
(1)填表:
图形编号 | ① | ② | ③ | ④ | ⑤ | ⑥ |
涂色的小方格数 |
(2)像这样,第 n 个图形要涂色的小方格数是__________,第100个图形要涂色的小方格数是____________