题目内容
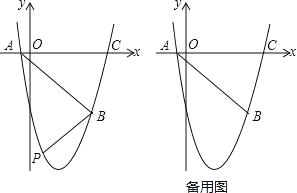
【题目】如图,已知一次函数y=﹣![]() x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=
x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=![]() MP,MB=
MP,MB=![]() OM,OE=
OM,OE=![]() ON,ND=
ON,ND=![]() NP.
NP.
(1)b= ;
(2)求证:四边形BCDE是平行四边形;
(3)在直线y=﹣![]() x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.
x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.

【答案】(1)3;(2)证明见解析;(3)在直线y=﹣![]() x+b上存在这样的点P,使四边形BCDE为正方形,P点坐标是(2,2)或(﹣6,6).
x+b上存在这样的点P,使四边形BCDE为正方形,P点坐标是(2,2)或(﹣6,6).
【解析】分析:(1)根据待定系数法,可得b的值;(2)根据矩形的判定与性质,可得PM与ON,PN与OM的关系,根据PC=![]() MP,MB=
MP,MB=![]() OM,OE=
OM,OE=![]() ON,NO=
ON,NO=![]() NP,可得PC与OE,CM与NE,BM与ND,OB与PD的关系,根据全等三角形的判定与性质,可得BE与CD,BC与DE的关系,根据平行四边形的判定,可得答案;(3)根据正方形的判定与性质,可得BE与BC的关系,∠CBM与∠EBO的关系,根据全等三角形的判定与性质,可得OE与BM的关系,可得P点坐标间的关系,可得答案.
NP,可得PC与OE,CM与NE,BM与ND,OB与PD的关系,根据全等三角形的判定与性质,可得BE与CD,BC与DE的关系,根据平行四边形的判定,可得答案;(3)根据正方形的判定与性质,可得BE与BC的关系,∠CBM与∠EBO的关系,根据全等三角形的判定与性质,可得OE与BM的关系,可得P点坐标间的关系,可得答案.
本题解析:
(1)一次函数y=﹣![]() x+b的图象过点A(0,3),
x+b的图象过点A(0,3),
3=﹣![]() ×0+b,解得b=3.
×0+b,解得b=3.
故答案为:3;
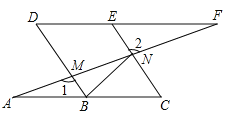
(2)证明:过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,
∴∠M=∠N=∠O=90°,
∴四边形PMON是矩形,
∴PM=ON,OM=PN,∠M=∠O=∠N=∠P=90°.
∵PC=![]() MP,MB=
MP,MB=![]() OM,OE=
OM,OE=![]() ON,NO=
ON,NO=![]() NP,
NP,
∴PC=OE,CM=NE,ND=BM,PD=OB,
在△OBE和△PDC中,
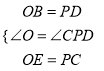 ,
,
∴△OBE≌△PDC(SAS),
BE=DC.
在△MBC和△NDE中,
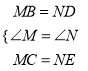 ,
,
∴△MBC≌△NDE(SAS),
DE=BC.
∵BE=DC,DE=BC,
∴四边形BCDE是平行四边形;
(3)设P点坐标(x,y),
当△OBE≌△MCB时,四边形BCDE为正方形,
OE=BM,
当点P在第一象限时,即![]() y=
y=![]() x,x=y.
x,x=y.
P点在直线上,
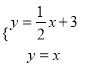 ,
,
解得![]() ,
,
当点P在第二象限时,﹣x=y
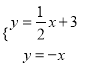 ,
,
解得![]()
在直线y=﹣![]() x+b上存在这样的点P,使四边形BCDE为正方形,P点坐标是(2,2)或(﹣6,6).
x+b上存在这样的点P,使四边形BCDE为正方形,P点坐标是(2,2)或(﹣6,6).