题目内容
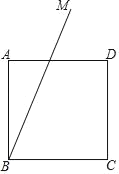
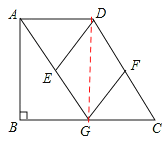
【题目】如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AG∥CD交BC于点G，点E、F分别为AG、CD的中点，连接DE、FG．
（1）求证：四边形DEGF是平行四边形；
（2）当点G是BC的中点时，求证：四边形DEGF是菱形．
【答案】证明见详解.
【解析】
（1）求出平行四边形AGCD，推出CD=AG，推出EG=DF，EG∥DF，根据平行四边形的判定推出即可.
（2）连接DG，求出∠DGC=90°，求出DF=GF，根据菱形的判定推出即可.
（1）∵AG∥DC，AD∥BC，
∴四边形AGCD是平行四边形
∴AG=DC
∵E、F分别为AG、DC的中点，
∴GE=
AG，DF=DC，
即GE=DF，GE∥DF
∴四边形DEGF是平行四边形
（2）连接DG，
∵四边形AGCD是平行四边形，
∴AD=CG
∵G为BC中点，
∴BG=CG=AD
∵AD∥BG，
∴四边形ABGD是平行四边形
∴AB∥DG
∵∠B=90°，
∴∠DGC=∠B=90°
∵F为CD中点，
∴GF=DF=CF，
即GF=DF
∵四边形DEGF是平行四边形，
∴四边形DEGF是菱形.
名校课堂系列答案
【题目】近来，校园安全问题引起了社会的极大关注．为了了解学生对安全知识的掌握情况，某校随机抽取了40名学生进行安全知识测试，测试成绩（百分制）如下：
78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 50
（1）本次测试属于 （填“普查”或“抽样调查”）；
（2）若按如下分数段整理成绩，则表中的a＝ ，b＝ ；
成绩x | 50≤x＜60 | 60≤x＜70 | 70≤x＜80 | 80≤x＜90 | 90≤x＜100 |
人数 | 1 | a | 18 | b | 3 |
（3）若用（2）中数据制作扇形统计图，求表示“70≤x＜80”的扇形的圆心角度数；
（4）已知该校共有2000名学生，若规定成绩80分及以上为优秀，估计该校学生对安全知识掌握情况是优秀的有多少人？
