Question

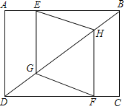
【题目】如图，正方形ABCD中，点E是AD边的中点，BD、CE交于点H，BE、AH交于点G，则下列结论：①AG⊥BE；②BE:BC=:2；③S△BHE=S△CHD；④∠AHB=∠EHD．其中正确的个数是

A.1B.2C.3D.4

Answer 1

【答案】D

【解析】

首先根据正方形的性质证得△BAE≌△CDE，推出∠ABE＝∠DCE，再证 △ADH≌△CDH，求得∠HAD＝∠HCD，推出∠ABE＝∠HAD:求出∠ABE+∠BAG＝90°;最后在△AGE中根据三角形的内角和是180°求得∠AGE＝90°即可得到①正确；

因为点E是AD边的中点，求出AB= 2AE，BE= AE

即可求得BE:BC=:2，故②正确；

根据 AD ∥BC，求出S△BDE=S△CDE，推出 S△BDE﹣S△DEH=S△CDE﹣S△DEH，

即；S△BHE=S△CHD，故③正确；

由∠AHD＝∠CHD，得到邻补角和对顶角相等得到∠AHB＝∠EHD，故④正确

∵四边形ABCD是正方形，E是AD边上的中点，

∴AE=DE，AB=CD，∠BAD=∠CDA=90°，

在△BAE和△CDE中

∵

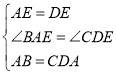
∴△BAE≌△CDE（SAS），

∴∠ABE=∠DCE，

∵四边形ABCD是正方形，

∴AD=DC，∠ADB=∠CDB=45°，

∵在△ADH和△CDH中，

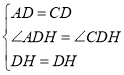
∴△ADH≌△CDH（SAS），

∴∠HAD=∠HCD，

∵∠ABE=∠DCE

∴∠ABE=∠HAD，

∵∠BAD=∠BAH+∠DAH=90°，

∴∠ABE+∠BAH=90°，
∴∠AGB=180°-90°=90°，
∴AG⊥BE，故①正确；

∵点E是AD边的中点，

∴AB= 2AE，

∴BE= AE

∴BE:BC=:2，故②正确；

∵AD∥BC，∴S△BDE=S△CDE，

∴S△BDE﹣S△DEH=S△CDE﹣S△DEH，

即；S△BHE=S△CHD，故③正确；

∵△ADH≌△CDH，

∴∠AHD=∠CHD，

∴∠AHB=∠CHB，

∵∠BHC=∠DHE，

∴∠AHB=∠EHD，故④正确；

故选：D．