题目内容
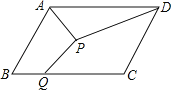
【题目】已知：如图，平行四边形ABCD中，M、N分别为AB和CD的中点．
（1）求证：四边形AMCN是平行四边形；
（2）当AC、BC满足怎样的数量关系时，四边形AMCN是矩形，请说明理由．
【答案】（1）见解析；（2）AC=BC，理由见解析
【解析】
（1）推导出AM=CN且AM∥CN，从而证四边形AMCN是平行四边形；
（2）当AC=BC时，可得出CM⊥AB，则有一个角是直角的平行四边形是矩形．
（1）证明∵四边形ABCD是平行四边形
∴AB＝CD，AB∥CD
∵M，N分别为AB和CD的中点
∴AM
AB，CNCD
∴AM＝CN，且AB∥CD
∴四边形AMCN是平行四边形
（2）答：AC=BC时，四边形AMCN是矩形
证明∵AC=BC，且M是BC的中点
∴CM⊥AB
即∠AMC＝90°
∴四边形AMCN是矩形
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
