题目内容
【题目】已知
的三条边长分别为6，8，12，过任一顶点画一条直线，将分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画（ ）
A.6条B.7条C.8条D.9条
【答案】B
【解析】
不妨设AB=6，AC=8，BC=12，分别作三边的垂直平分线，则可得三条，再分以AB、AC为腰和底进行讨论，可得出结论．
解：不妨设AB=6，AC=8，BC=12，分别作三边的垂直平分线，
如图1，则BD=AD，EA=EC，FB=FC，可知AE、BF、AD满足条件；
当AB为腰时，以点A为圆心，AB为半径画圆，分别交BC、AC于点G、H，
以B为圆心，AB为半径，交BC于点J，如图2，则AB=AG，AB=AH，BA=BJ，满足条件；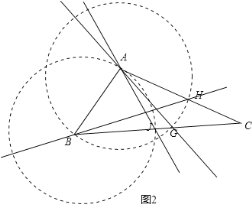
当AC为腰时，如图3，以点C为圆心，CA为半径画圆，交BC于点M，则CA=CM，满足条件；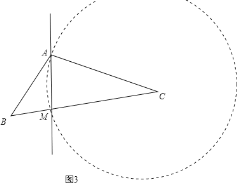
当A为圆心AC为半径画圆时，与AB、BC都没有交点，
因为BC为最长的边，所以不可能存在以BC为腰的等腰三角形，
综上可知满足条件的直线共有7条.
故选B．
练习册系列答案
相关题目
