题目内容
【题目】如图,在ABCD中,AB=4,BC=6,∠ABC=60°,点P为ABCD内一点,点Q在BC边上,则PA+PD+PQ的最小值为( )
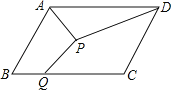
A.![]() B.6+2
B.6+2![]() C.5
C.5![]() D.10
D.10
【答案】C
【解析】
如下图,将△APD绕点A逆时针旋转60°至△AFE处,通过边长转换,可将PA+PD+PQ转化为PF+EF+PQ的形式,再利根据两点之间线段最短,得出最小值.
如下图,将△APD绕点A逆时针旋转60°至△AFE处,连接FP,过点E作BC的垂线,交BC于点G,AD于点H,过点A作BC的垂线,交BC于点K
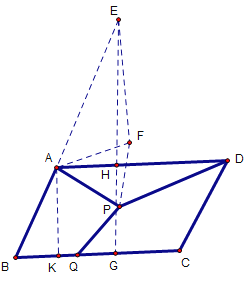
∵△AFE是△APD绕点A逆时针旋转60°得到
∴∠FAP=60°,∠EAD=60°,AF=AP,EF=PD
∴△APF是等边三角形,∴AP=PF
∴PA+PD+PQ=PF+FE+PQ≥EG
∵四边形ABCD是平行四边形,BC=6
∴AE=AD=BC=6,AD∥BC
∴在Rt△AHE中,AH=3,EH=3![]()
∵HG⊥BC,AK⊥BC,AD∥BC
∴AK⊥AD,GH⊥AD,∴AK=HG
∵∠ABC=60°,AB=4
∴在Rt△ABK中,BK=2,AK=2![]()
∴HG=2![]()
∴EG=3![]()
故选:C

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
【题目】近年来,青少年中的近视眼和肥胖案例日趋增多,人们普遍意识到健康的身体是学习的保障,所以体育活动越来越受重视.某商店分两次购进跳绳和足球两种商品进行销售,每次购进同一种商品的进价相同,具体情况如下表所示.
购进数量(件) | 购进所需费用(元) | ||
跳绳 | 足球 | ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1)跳绳和足球两种商品每件的进价分别是多少元?
(2)商店计划用5300元的资金进行第三次进货,共购进跳绳和足球两种商品100件,其中要求足球的数量不少于跳绳的数量,有哪几种进货方案?