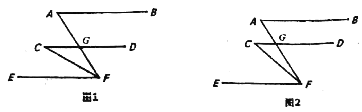题目内容
【题目】如图,在平行四边形ABCD中,CE平分∠BCD与AB交于点E,BF平分∠ABC与AD交于点F,若![]() ,EF=4,则CD长为________.
,EF=4,则CD长为________.

【答案】7
【解析】
已知ABCD是平行四边形,可得∠AFB=∠FBC,BF平分∠ABC,根据角平分线性质定理可得∠ABF=∠FBC,即可得出∠AFB=∠ABF,AB=AF,同理可得∠DEC=∠DCE,ED=CD
设AB=CD=x,AD=10,EF=4,则FD =10-x,ED=14-x,根据ED=CD,可得14-x=x,即可求出x值.
∵ABCD是平行四边形
∴AD∥BC
∴∠AFB=∠FBC
∵BF平分∠ABC
∴∠ABF=∠FBC
∴∠AFB=∠ABF
∴AB=AF
∵AD∥BC
∴∠DEC=∠ECB
∵CE平分∠BCD
∴∠DCE=∠ECB
∴∠DEC=∠DCE
∴ED=CD
设AB=CD=x,AD=10,EF=4
则FD=AD-AF=AD-AB=10-x
∴ED=EF+FD=4+10-x=14-x
∴14-x=x
解得x=7
故答案为:7

练习册系列答案
相关题目