Question

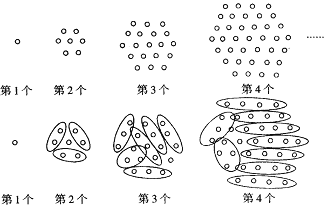
【题目】小明同学在寻找下面图中小圆圈个数的规律时，利用了下面图中“分块计数法”，根据小明的方法，猜想并判断下列说法不正确的是( )

A.第5个图形有61个小圆圈B.第6个图形有91个小圆圈

C.某个图小圆圈的个数可以为271D.某个图小圆圈的个数可以为621

Answer 1

【答案】D

【解析】

设第n个图形中小圆圈的个数为an个（n为正整数），根据给定几个图形中小圆圈数量的变化可找出变化规律“an＝3n23n＋1（n为正整数）”，分别代入n＝5，n＝6，an＝271，an＝621求出an（或n）即可得出结论．

设第n个图形中小圆圈的个数为an个（n为正整数）．
观察图形，可知：a1＝1，a2＝7＝2×3＋1，a3＝19＝3×6＋1，a4＝37＝4×9＋1，…，
∴an＝n3（n1）＋1＝3n23n＋1（n为正整数）．
当n＝5时，a5＝3×523×5＋1＝61；
当n＝6时，a6＝3×623×6＋1＝91；
当3n23n＋1＝271时，解得：n1＝9（舍去），n2＝10；
当3n23n＋1＝621时，解得：n1＝（舍去），n2＝．
故选：D．