题目内容
【题目】有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的立杆上点T处汇合.如图所示为截面图,以水平方向为x轴,喷水池中心为原点建立直角坐标系
(1)求水柱所在抛物线(第一象限部分)的函数解析式
(2)正在喷水时,身高1.8米的人,应站在离水池中心多远的地方就能不被淋湿？
(3)在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心的立杆上点T处汇合,请探究扩建后喷水池水柱的最大高度
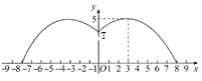
【答案】（1）
；（2）为了不被淋湿，身高1.8米的人站立时必须在离水池中心7米以内；（3）
【解析】
（1）根据顶点坐标可设二次函数的顶点式，代入（8,0）即可求得a，此题得解；
（2）利用二次函数图象上点的坐标特征，求出当y=1.8时x的值，由此即可得出结论；
（3）利用二次函数图象上点的坐标特征可求出抛物线与y轴交点坐标，由抛物线的形状不变可设扩建后水柱所在抛物线（第一象限部分）的函数表达式为
，代入点（16,0）可求出b的值，再利用配方法将二次函数表达式变形为顶点式，即可得出结论.
（1）解：设水柱所在抛物线（第一象限部分）的函数表达式为
将（8，0）代入
，得：
25a+5=0
解得：
∴水柱所在抛物线（第一象限部分）的函数表达式为
（2）解：当
时，有
解得：
∴为了不被淋湿，身高1.8米的人站立时必须在离水池中心7米以内.
（3）解：当x=0时，
设扩建后水柱所在抛物线（第一象限部分）的函数表达式为
∵该函数图象经过点（16,0）
∴
解得：
∴扩建后水柱所在抛物线（第一象限部分）的函数表达式为
∴扩建后喷水池水柱的最大高度为
练习册系列答案
相关题目
