��Ŀ����
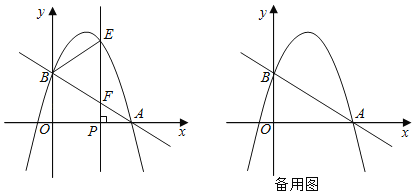
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() �ֱ�x�ᣬy���ڵ�A��B��������y����x2+bx+c������A��B����P��x����һ�����㣬����P����ֱ��x���ֱ�߷ֱ������ߺ�ֱ��AB�ڵ�E�͵�F.���P�ĺ�����Ϊm.
�ֱ�x�ᣬy���ڵ�A��B��������y����x2+bx+c������A��B����P��x����һ�����㣬����P����ֱ��x���ֱ�߷ֱ������ߺ�ֱ��AB�ڵ�E�͵�F.���P�ĺ�����Ϊm.
(1)����������������Ӧ�ĺ�������ʽ.
(2)��P���߶�OA��ʱ������B��E��FΪ��������������FPA���ƣ���m��ֵ��
(3)��E��F��P��������ǡ��һ�����������������߶ε��е�(�����غϳ���)����E��F��P����Ϊ���������.ֱ��д��E��F��P�����Ϊ���������ʱm��ֵ.
���𰸡�(1)y����x2+![]() x+2��(2)m��
x+2��(2)m��![]() ��
��![]() ��(3) -1��-
��(3) -1��-![]() ��
��![]() .
.
��������
��1��![]() ��x�ᣬy���ڵ�A��B�������A��B�����꣬�ɵ�c��2���������߱���ʽΪ��y����x2+bx+2������A�����������ʽ��������⣻
��x�ᣬy���ڵ�A��B�������A��B�����꣬�ɵ�c��2���������߱���ʽΪ��y����x2+bx+2������A�����������ʽ��������⣻
��2��������EBFΪֱ��ʱ����tan��BEF��![]() ����BE2��4BF2�����ݹ��ɶ����з�����⼴�ɣ�������BEFΪֱ��ʱ����EF��
����BE2��4BF2�����ݹ��ɶ����з�����⼴�ɣ�������BEFΪֱ��ʱ����EF��![]() BE�����ͬ��������⣻
BE�����ͬ��������⣻
��3����m�ɱ�ʾ��P��F��E�����꣬�������֪��FΪ�߶�PE���е㡢PΪ�߶�EF���е��EΪ�߶�PF���е㣬�ɷֱ�õ�����m�ķ��̣������m��ֵ��
�⣺��1����x=0����![]() ����
����![]() =2.
=2.
��y=0����![]() ����
����![]() ����x=4.
����x=4.
���A��B������ֱ�Ϊ(4��0)��(0��2)��
��c��2��
�������߱���ʽΪ��y����x2+bx+2��
����A�����������ʽ�ã�
0����16+4b+2��
��b��![]() ��
��
�������ߵı���ʽΪ��y����x2+![]() x+2��
x+2��
��2��tan��OAB��![]() ��
��![]() ��
��
��P�ĺ�����Ϊm�����E��F������ֱ�Ϊ��(m����m2+![]() m+2)��(m����
m+2)��(m����![]() m+2)��
m+2)��
������EBFΪֱ��ʱ��
��B��E��FΪ���������������FPA���ƣ�����BEF����OAB��
��tan��BEF��![]() ����BE2��4BF2��
����BE2��4BF2��
����m2+(��m2+![]() m+2
m+2![]() m��2)2��4[m2+(��
m��2)2��4[m2+(��![]() m+2��2)2]��
m+2��2)2]��
��ã�m��![]() ��
��![]() (��ȥ
(��ȥ![]() )��
)��
������BEFΪֱ��ʱ��
��EF��![]() BE��
BE��
�ੁm2+![]() m+2
m+2![]() m��2=
m��2=![]() m��
m��
���
m1=![]() ��m2=0����ȥ��.
��m2=0����ȥ��.
���ϣ�m��![]() ��
��![]() ��
��
��3����P�ĺ�����Ϊm�����P��E��F������ֱ�Ϊ��(m��0)��(m����m2+![]() m+2)��(m����
m+2)��(m����![]() m+2)��
m+2)��
��E��F��P����Ϊ����г������
����FΪ�߶�PE���е㡢PΪ�߶�FE���е��EΪ�߶�PF���е㣬
��FΪ�߶�PE���е�ʱ������2��-![]() m+2��=-m2+
m+2��=-m2+![]() m+2�����m=4�������غϣ���ȥ����m=
m+2�����m=4�������غϣ���ȥ����m=![]() ��
��
��PΪ�߶�FE���е�ʱ������-![]() m+2+��-m2+
m+2+��-m2+![]() m+2��=0�����m=4����ȥ����m=-1��
m+2��=0�����m=4����ȥ����m=-1��
��EΪ�߶�FP���е�ʱ������-![]() m+2=2��-m2+
m+2=2��-m2+![]() m+2�������m=4����ȥ����m=-
m+2�������m=4����ȥ����m=-![]() ��
��
���Ͽ�֪��E��F��P�����Ϊ����г����ʱm��ֵΪ-1��-![]() ��
��![]() ��
��

 ��У����ϵ�д�
��У����ϵ�д�