题目内容
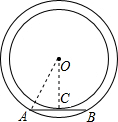
如图所示,两同心圆O,大圆的弦AB切小圆于点C,且AB=4,求圆环的面积.


连接OC,OA,
∵大圆的弦AB切小圆于点C,
∴OC⊥AB,
∴AC=BC=
AB=
×4=2,
∵在Rt△OAC中,OA2-OC2=AC2=4,
∴圆环的面积为:πOA2-πOC2=π(OA2-OC2)=4π.
∵大圆的弦AB切小圆于点C,
∴OC⊥AB,
∴AC=BC=
| 1 |
| 2 |
| 1 |
| 2 |
∵在Rt△OAC中,OA2-OC2=AC2=4,
∴圆环的面积为:πOA2-πOC2=π(OA2-OC2)=4π.


练习册系列答案
相关题目







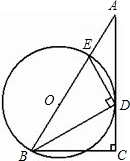 的外接圆.
的外接圆.