题目内容
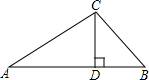
如图所示，在四边形ABCD中，AD∥BC，AB⊥AC，AD⊥DC，∠B=45°，CD=2cm，求BC的长．
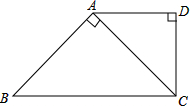
∵AB⊥AC，∠B=45°，
∴∠ACB=45°，
∴△ABC是等腰直角三角形，且AB=AC，
∵AD∥BC，
∴∠DAC=∠ACB=45°，
∵AD⊥DC，
∴△ADC是等腰直角三角形，
∵CD=2cm，
∴AC=
=2
（cm），
∴BC=
=4（cm）．
∴∠ACB=45°，
∴△ABC是等腰直角三角形，且AB=AC，
∵AD∥BC，
∴∠DAC=∠ACB=45°，
∵AD⊥DC，
∴△ADC是等腰直角三角形，
∵CD=2cm，
∴AC=
| AD2+CD2 |
| 2 |
∴BC=
| AB2+AC2 |
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案
相关题目
