题目内容
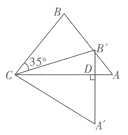
【题目】如图,AB为圆O的直径,PD切圆O于点C,交AB的延长线于点D,且 ![]() D=2
D=2 ![]() CAD.
CAD.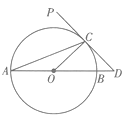
(1)求 ![]() D的度数;
D的度数;
(2)若CD=2,求BD的长.
【答案】
(1)解:∵ ![]() 和
和 ![]() 分别是弧
分别是弧 ![]() 所对的圆心角和圆周角,∴
所对的圆心角和圆周角,∴ ![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
∵ ![]() 与⊙O相切于点
与⊙O相切于点 ![]() ,
,
∴ ![]() ,
,
∴![]() .
.
∴ ![]() 是等腰直角三角形,
是等腰直角三角形,
∴ ![]()
(2)解:由第(1)问可知 ![]() 是等腰直角三角形,∴
是等腰直角三角形,∴ ![]() ,
,
∴ ![]() ,
,
由勾股定理得 ![]()
![]()
![]() ,
,
∴ ![]()
【解析】(1)根据同弧所对的圆周角等于圆心角的一半得出∠ C O D = 2 ∠ A ,又因∠ D = 2 ∠ A ,从而得出∠ C O D = ∠ D ;根据圆的切线垂直于经过切点的半径得出O C ⊥ P D ,故∠ O C D = 90 ° ,从而得出△ O C D 是等腰直角三角形,故∠ D = 45 ° ;
(2)根据由第(1)问可知 △ O C D 是等腰直角三角形及同圆的半径相等得出O C = C D = 2 =OB;根据勾股定理得出OD的长度,再根据线段的和差得出BD的长度。

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
【题目】甲,乙两人是NBA联盟凯尔特人队的两位明星球员,两人在前五个赛季的罚球
命中率如下表所示:
甲球员的命中率(%) | 87 | 86 | 83 | 85 | 79 |
乙球员的命中率(%) | 87 | 85 | 84 | 80 | 84 |
(1)分别求出甲,乙两位球员在前五个赛季罚球的平均命中率;
(2)在某场比赛中,因对方球员技术犯规需要凯尔特人队选派一名队员进行罚球,你认为甲,乙两位球员谁来罚球更好?(请通过计算说明理由)