题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() 平分
平分![]() ,分别交
,分别交![]() ,
,![]() 于
于![]() ,
,![]() ,
,![]() 于
于![]() .连接
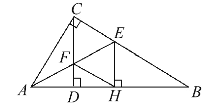
.连接![]() ,求证:四边形
,求证:四边形![]() 是菱形.
是菱形.
【答案】详见解析
【解析】
求出CE=EH,AC=AH,证△CAF≌△HAF,推出∠ACD=∠AHF,求出∠B=∠ACD=∠FHA,推出HF∥CE,推出CF∥EH,得出平行四边形CFHE,根据菱形判定推出即可.
∵∠ACB=90°,AE平分∠BAC,EH⊥AB,
∴CE=EH,
在Rt△ACE和Rt△AHE中,AE=AE,CE=EH,
∴Rt△ACE≌ Rt△AHE(HL),
∴AC=AH,
∵AE平分∠CAB,
∴∠CAF=∠HAF,
在△CAF和△HAF中,
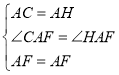 ,
,
∴△CAF≌△HAF(SAS),
∴∠ACD=∠AHF,
∵CD⊥AB,∠ACB=90°,
∴∠CDA=∠ACB=90°,
∴∠B+∠CAB=90°,∠CAB+∠ACD=90°,
∴∠ACD=∠B=∠AHF,
∴FH∥CE,
∵CD⊥AB,EH⊥AB,
∴CF∥EH,
∴四边形CFHE是平行四边形,
∵CE=EH,
∴四边形CFHE是菱形.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
【题目】李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩.她从中随机调查了若干名女生的测试成绩(单位:米),并将统计结果绘制成了如下的统计图表(内容不完整).
测试成绩 |
|
|
|
|
| 合计 |
频数 | 3 | 27 | 9 | m | 1 | n |

请你结合图表中所提供的信息,回答下列问题:
(1)表中m= ,n= ;
(2)请补全频数分布直方图;
(3)在扇形统计图中,![]() 这一组所占圆心角的度数为 度;
这一组所占圆心角的度数为 度;
(4)如果掷实心球的成绩达到6米或6米以上为优秀,请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数.