题目内容
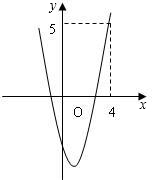
已知二次函数y=x2-2x+c的图象如图所示．
（1）求c的值和抛物线的顶点坐标；
（2）求抛物线与x轴的交点坐标．
（1）求c的值和抛物线的顶点坐标；
（2）求抛物线与x轴的交点坐标．
（1）∵图象过点（4，5），（1分）
∴5=16-8+c．
解得：c=-3． （2分）
∴y=x2-2x-3．（1分）
∵y=x2-2x-3=（x-1）2-4，
∴抛物线的顶点坐标是（1，-4）．（2分）
（2）当y=0时，x2-2x-3=0． （1分）
解得：x1=-1，x2=3．（2分）
∴抛物线与x轴的交点坐标为（-1，0）和（3，0）．（1分）
∴5=16-8+c．
解得：c=-3． （2分）
∴y=x2-2x-3．（1分）
∵y=x2-2x-3=（x-1）2-4，
∴抛物线的顶点坐标是（1，-4）．（2分）
（2）当y=0时，x2-2x-3=0． （1分）
解得：x1=-1，x2=3．（2分）
∴抛物线与x轴的交点坐标为（-1，0）和（3，0）．（1分）
练习册系列答案
相关题目
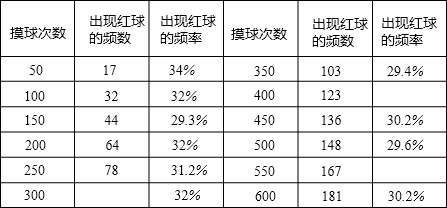
规则公平，请你制订一个不公平的游戏规则．
