ЬтФПФкШн
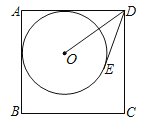
ЁОЬтФПЁПШчЭМ1ЃЌЁїABCжаЃЌACЃНBCЃЌЁЯACBЃН90ЁуЃЌЕуPЮЊABЩЯвЛЕуЃЈвьгкAЁЂBЃЉЃЌBDЁЭжБЯпCPгкDЃЌAEЁЭжБЯпCPгкEЃЌЕуFЮЊABЕФжаЕуЃЌСЌНгDFЃЎ
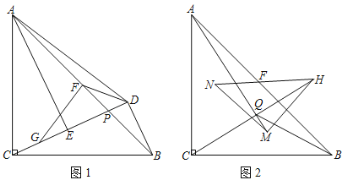
ЃЈ1ЃЉПЩвдАбЁїACEШЦЕуFФцЪБеыа§зЊЁЁ ЁЁЖШЃЈЖШЪ§ВЛГЌЙ§180ЁуЃЉКЭЁїЁЁ ЁЁжиКЯЃЌдђЁЯFDEЃНЁЁ ЁЁЁуЃЎ
ЃЈ2ЃЉШЁCEЕФжаЕуGЃЌСЌНгADЁЂFGЃЌЧѓжЄЃКADЃН2FGЃЎ
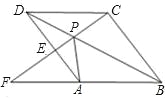
ЃЈ3ЃЉШчЭМ2ЃЌABЃН8ЃЌЕШбќжБНЧЁїMNHЕФаББпNHЕФжаЕувВЮЊЕуFЃЌжБЯпAMКЭжБЯпCHНЛгкЕуQЃЌСЌНгBQЃЌЕБЁїMNHШЦЕуFа§зЊвЛжмЪБЃЌЧыжБНгаДГіBQГЄЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉ90ЃЌCBDЃЌ45ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉ2![]() -2
-2![]() ЁмBQЁм2
ЁмBQЁм2![]() +2
+2![]()
ЁОНтЮіЁП
(1)гЩЕШбќжБНЧШ§НЧаЮЕФаджЪПЩЕУCF=AF=BFЃЌCFЁЭBFЃЌгЩЁАAASЁБПЩжЄЁїACEЁеЁїCBDЃЌдђПЩвдАбЁїACEШЦЕуFФцЪБеыа§зЊ90ЖШКЭЁїCBDжиКЯЃЌПЩЕУCE=DBЃЌEF=DFЃЌПЩжЄЁїCFEЁеЁїBFDЃЌПЩЕУЁЯCFE=ЁЯBFDЃЌПЩжЄЁЯEFD=90ЁуЃЌПЩЧѓНтЃЛ
(2)ШЁBDжаЕуHЃЌСЌНгFHЃЌгЩжаЕуЖЈвхКЭШ§НЧаЮжаЮЛЯпЖЈРэПЩЕУCG=![]() CE=
CE=![]() BD=BHЃЌADЁЮFHЃЌAD=2FHЃЌгЩЁАSASЁБПЩжЄЁїCFGЁеЁїBFHЃЌПЩЕУGF=FHЃЌПЩЕУAD=2FGЃЛ
BD=BHЃЌADЁЮFHЃЌAD=2FHЃЌгЩЁАSASЁБПЩжЄЁїCFGЁеЁїBFHЃЌПЩЕУGF=FHЃЌПЩЕУAD=2FGЃЛ
(3)ШчЭМ2ЃЌСЌНгCFЃЌMFЃЌгЩШЋЕШШ§НЧаЮЕФаджЪПЩЧѓЁЯAQC=90ЁуЃЌПЩЕУЕуQдквдACЮЊжБОЖЕФдВЩЯдЫЖЏЃЌМДПЩЧѓНтЃЎ
(1)ШчЭМ1ЃЌСЌНгCFЃЌEFЃЌ
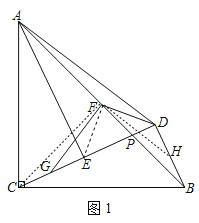
ЁпAC=BCЃЌЁЯACB=90ЁуЃЌЕуFЮЊABЕФжаЕуЃЌ
ЁрCF=AF=BFЃЌCFЁЭBFЃЌ
ЁпAEЁЭCDЃЌBDЁЭCDЃЌ
ЁрЁЯAEC=ЁЯCDB=ЁЯACB=90ЁуЃЌ
ЁрЁЯACE+ЁЯCAE=90ЁуЃЌЁЯACE+ЁЯDCB=90ЁуЃЌ
ЁрЁЯCAE=ЁЯDCBЃЌЧвAC=BCЃЌЁЯAEC=ЁЯCDB=90ЁуЃЌ
ЁрЁїACEЁеЁїCBD(AAS)
ЁрПЩвдАбЁїACEШЦЕуFФцЪБеыа§зЊ90ЖШКЭЁїCBDжиКЯЃЌ
ЁрCE=DBЃЌEF=DFЃЌЧвCF=BFЃЌ
ЁрЁїCFEЁеЁїBFD(SSS)
ЁрЁЯCFE=ЁЯBFDЃЌЧвЁЯCFE+ЁЯEFB=90ЁуЃЌ
ЁрЁЯBFD+ЁЯEFB=90ЁуЃЌ
ЁрЁЯEFD=90ЁуЃЌЧвEF=DFЃЌ
ЁрЁЯFDE=45ЁуЃЌ
ЙЪД№АИЮЊЃК90ЃЌCBDЃЌ45ЃЛ
(2)ШчЭМ1ЃЌШЁBDжаЕуHЃЌСЌНгFHЃЌ
ЁпЕуGЪЧCEжаЕуЃЌЕуHЪЧBDжаЕуЃЌЕуFЪЧABжаЕуЃЌЧвCE=BDЃЌ
ЁрCG=![]() CE=
CE=![]() BD=BHЃЌADЁЮFHЃЌAD=2FHЃЌ
BD=BHЃЌADЁЮFHЃЌAD=2FHЃЌ
ЁпЁїCFEЁеЁїBFDЃЌ
ЁрЁЯFCG=ЁЯFBHЃЌЧвCG=BHЃЌCF=BFЃЌ
ЁрЁїCFGЁеЁїBFH(SAS)
ЁрGF=FHЃЌ
ЁрAD=2FGЃЛ
(3)ШчЭМ2ЃЌСЌНгCFЃЌMFЃЌ
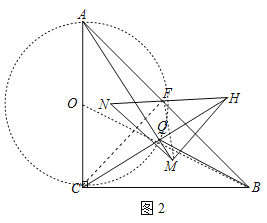
ЁпAC=BCЃЌЁЯACB=90ЁуЃЌЕуFЪЧABжаЕуЃЌAB=8ЃЌ
ЁрAF=CF=BF=4ЃЌCFЁЭABЃЌAC=BC=4![]() ЃЌ
ЃЌ
ЁпMN=MHЃЌЁЯNMH=90ЁуЃЌЕуFЪЧNHжаЕуЃЌ
ЁрNF=FH=FMЃЌMFЁЭNHЃЌ
ЁрЁЯMFH=ЁЯAFC=90ЁуЃЌ
ЁрЁЯAFM=ЁЯCFHЃЌЧвAF=CFЃЌFH=FMЃЌ
ЁрЁїAFMЁеЁїCFH(SAS)
ЁрЁЯFAM=ЁЯFCHЃЌ
ЁпЁЯFAM+ЁЯCAM+ЁЯACF=90ЁуЃЌ
ЁрЁЯCAM+ЁЯACF+ЁЯFCH=90ЁуЃЌ
ЁрЁЯAQC=90ЁуЃЌ
ЁрЕуQдквдACЮЊжБОЖЕФдВЩЯдЫЖЏЃЌ
ЁрЕБЕуQдкBOЕФбгГЄЯпЩЯЪБЃЌBQзюДѓЃЛЕБЕуQдкЯпЖЮBOЩЯЪБЃЌBQзюаЁЃЎ
ШЁACжаЕуOЃЌСЌНгBOЃЌ
ЁрCO=2![]() ЃЌ
ЃЌ
ЁрBO=![]() =
=![]() =2
=2![]() ЃЌ
ЃЌ
ЁрBQГЄЕФШЁжЕЗЖЮЇЮЊ![]()