ЬтФПФкШн
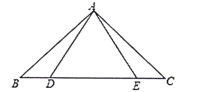
ЁОЬтФПЁПШчЭМЂйЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНax2ЃЋbxЃЋcЃЈaЁй0ЃЉОЙ§ЕуDЃЈ2ЃЌ4ЃЉЃЌгыxжсНЛгкAЃЌBСНЕуЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ4ЃЉЃЌСЌНгACЃЌCDЃЌBCЃЌ ЦфЧвAC=5ЃЎ
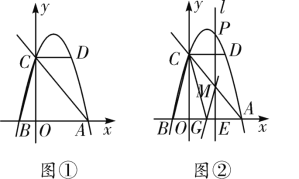
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌЕуPЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпlЃЌlЗжБ№НЛxжсгкЕуEЃЌНЛжБЯпACгкЕуMЃЎЩшЕуPЕФКсзјБъЮЊmЃЎЕБ0<mЁм2ЪБЃЌЙ§ЕуMзїMGЁЮBCЃЌMGНЛxжсгкЕуGЃЌСЌНгGCЃЌдђmЮЊКЮжЕЪБЃЌЁїGMCЕФУцЛ§ШЁЕУзюДѓжЕЃЌВЂЧѓГіетИізюДѓжЕЃЛ
ЃЈ3ЃЉЕБ-1<mЁм2ЪБЃЌЪЧЗёДцдкЪЕЪ§mЃЌЪЙЕУвдPЃЌCЃЌMЮЊЖЅЕуЕФШ§НЧаЮКЭЁїAEMЯрЫЦЃПШєДцдкЃЌЧѓГіЯргІmЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=Љ![]() x2+
x2+![]() x+4ЃЛЃЈ2ЃЉЕБm=
x+4ЃЛЃЈ2ЃЉЕБm=![]() ЪБЃЌSзюДѓЃЌМДSзюДѓ=2ЃЛЃЈ3ЃЉ2Лђ
ЪБЃЌSзюДѓЃЌМДSзюДѓ=2ЃЛЃЈ3ЃЉ2Лђ![]()
ЁОНтЮіЁП
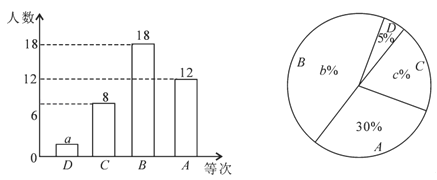
ЃЈ1ЃЉЯШЭЈЙ§ЙДЙЩЖЈРэЧѓЕФЕуAЕФзјБъЃЌАбAЁЂCЁЂDШ§ЕузјБъДњШыМДПЩЧѓЕУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉгЩAЁЂCзјБъПЩЧѓЕУжБЯпACНтЮіЪНЃЌдйгУmБэЪОГіЕуMзјБъЃЌБэЪОГіMEЃЌдйгЩЁїBCOЁзЁїGMEПЩБэЪОГіGEЃЌЧѓЕУOGЃЌдйРћгУУцЛ§ЕФКЭВюПЩЕУЕНЁїGMCЕФУцЛ§ЃЌРћгУЖўДЮКЏЪ§ЕФаджЪПЩЧѓЕУЦфзюДѓжЕЃЛ
ЃЈ3ЃЉЗжЁЯCPMЃН90ЁуКЭЁЯPCMЃН90ЁуСНжжЧщПіЃЌЕБЁЯCPMЃН90ЁуЪБЃЌПЩЕУPCЁЮxжсЃЌШнвзЧѓЕУPЕузјБъКЭmЕФжЕЃЛЕБЁЯPCMЃН90ЁуЪБЃЌЩшPCНЛxжсгкЕуFЃЌПЩРћгУЯрЫЦШ§НЧаЮЕФаджЪЯШЧѓЕУFЕузјБъЃЌПЩЧѓЕУжБЯпCFЕФНтЮіЪНЃЌдйСЊСЂХзЮяЯпНтЮіЪНПЩЧѓЕУPЕузјБъКЭЯргІЕФmЕФжЕЃЎ
НтЃЈ1ЃЉЁпЕуCЃЈ0ЃЌ4ЃЉЃЌ
ЁрOCЃН4ЃЌ
ЁпACЃН5ЃЌ
ЁрдкRtЁїAOCжаЃЌЁЯAOCЃН90Ёу
OAЃН![]()
Ёр AЃЈ3ЃЌ0ЃЉ
НЋAЃЈ3ЃЌ0ЃЉЁЂCЃЈ0ЃЌ4ЃЉDЃЈ2ЃЌ4ЃЉДњШыХзЮяЯпyЃНax2ЃЋbxЃЋcЃЈaЁй0ЃЉжа
ЕУ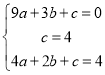 ЃЌ
ЃЌ
НтЕУЃЌ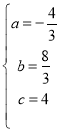
ЁрХзЮяЯпНтЮіЪНЮЊyЃНЃ![]() x2ЃЋ
x2ЃЋ![]() xЃЋ4ЃЛ
xЃЋ4ЃЛ
ЃЈ2ЃЉгЩAЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌ4ЃЉПЩЕУжБЯпACНтЮіЪНЮЊyЃНЃ![]() xЃЋ4ЃЌ
xЃЋ4ЃЌ
ЁрMзјБъЮЊЃЈmЃЌЃ![]() mЃЋ4ЃЉЃЌ
mЃЋ4ЃЉЃЌ
ЁпMGЁЮBCЃЌ
ЁрЁЯCBOЃНЁЯMGEЃЌЧвЁЯCOBЃНЁЯMEGЃН90ЁуЃЌ
ЁрЁїBCOЁзЁїGMEЃЌ
Ёр![]() ЃЌМД
ЃЌМД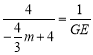 ЃЌ
ЃЌ
ЁрGEЃНЃ![]() mЃЋ1ЃЌ
mЃЋ1ЃЌ
ЁрOGЃНOEЃGEЃН![]() mЃ1
mЃ1
Ёр![]()
![]()
![]()
![]() ЃЌ
ЃЌ
ЁрЕБmЃН![]() ЪБЃЌSзюДѓЃЌМДSзюДѓЃН2ЃЛ
ЪБЃЌSзюДѓЃЌМДSзюДѓЃН2ЃЛ
ЃЈ3ЃЉИљОнЬтвтПЩжЊЁїAEMЪЧжБНЧШ§НЧаЮЃЌЖјЁїMPCжаЃЌЁЯPMCЃНЁЯAMEЮЊШёНЧЃЌ
ЁрЁїPCMЕФжБНЧЖЅЕуПЩФмЪЧPЛђCЃЌ
ЕквЛжжЧщПіЃКЕБЁЯCMPMЃН90ЁуЪБЃЌШчЭМЃЌ
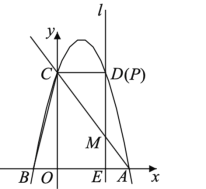
дђCPЁЮxжсЃЌДЫЪБЕуPгыЕуDжиКЯЃЌ
ЁрЕуPЃЈ2ЃЌ4ЃЉЃЌДЫЪБmЃН2ЃЛ
ЕкЖўжжЧщПіЃКЕБЁЯPCMЃН90ЁуЪБЃЌШчЭМЃЌ
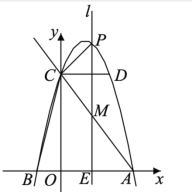
ШчЭМЃЌбгГЄPCНЛxжсгкЕуFЃЌгЩЁїFCAЁзЁїCOAЃЌЕУ![]() ЃЌ
ЃЌ
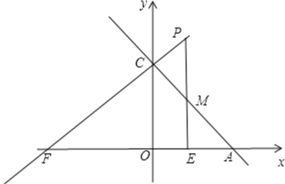
ЁрAFЃН![]() ЃЌ
ЃЌ
ЁрOFЃН![]() ЃЌ
ЃЌ
ЁрFЃЈЃ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ЁржБЯпCFЕФНтЮіЪНЮЊyЃН![]() xЃЋ4ЃЌ
xЃЋ4ЃЌ
СЊСЂжБЯпCFКЭХзЮяЯпНтЮіЪНПЩЕУ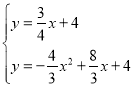 ЃЌ
ЃЌ
НтЕУ ЃЌ
ЃЌ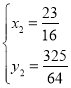 ЃЌ
ЃЌ
ЁрPзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌДЫЪБmЃН
ЃЉЃЌДЫЪБmЃН![]() ЃЛ
ЃЛ
злЩЯПЩжЊДцдкТњзуЬѕМўЕФЪЕЪ§mЃЌЦфжЕЮЊ2Лђ![]()

 ОйвЛЗДШ§ЦкФЉАйЗжГхДЬОэЯЕСаД№АИ
ОйвЛЗДШ§ЦкФЉАйЗжГхДЬОэЯЕСаД№АИ