题目内容
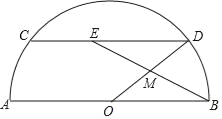
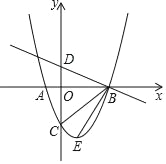
【题目】如图,抛物线y=ax2+bx﹣3,顶点为E,该抛物线与x轴交于A,B两点,与y轴交子点C,且OB=OC=3OA,直线y=﹣![]() x+1与y轴交于点D.求∠DBC﹣∠CBE=_____.
x+1与y轴交于点D.求∠DBC﹣∠CBE=_____.
【答案】45°.
【解析】
先求出点D、点C的坐标,得出点B、A的坐标,求出抛物线的解析式,得出抛物线的顶点坐标,根据勾股定理求出BC、CE、BE,由勾股定理的逆定理证明△BCE为直角三角形,∠BCE=90°,由三角函数证出∠DBO=∠CBE,即可得出∠DBC-∠CBE=∠DBC-∠DBO=∠OBC=45°.
将x=0代入y=![]() x+1,y=1,
x+1,y=1,
∴D(0,1),
将x=0代入y=ax2+bx-3得:y=-3,
∴C(0,-3),
∵OB=OC=3OA,
∴B(3,0),A(-1,0),∠OBC=45°,
对于直线y=![]() x+1,
x+1,
当y=0时,x=3,
∴直线y=![]() x+1过点B.
x+1过点B.
将点C(0,-3)的坐标代入y=a(x+1)(x-3),
得:a=1,
∴抛物线的解析式为:y=x2-2x-3=(x-1)2-4,
∴抛物线y=x2-2x-3的顶点为E(1,-4).
于是由勾股定理得:
BC=3![]() ,CE=
,CE=![]() ,BE=2
,BE=2![]() .
.
∵BC2+CE2=BE2,
∴△BCE为直角三角形,∠BCE=90°,
因此tan∠CBE=![]() =
=![]() .
.
又tan∠DBO=![]() =
=![]() ,
,
则∠DBO=∠CBE,
∴∠DBC-∠CBE=∠DBC-∠DBO=∠OBC=45°.
故答案为:45°.

 快乐小博士巩固与提高系列答案
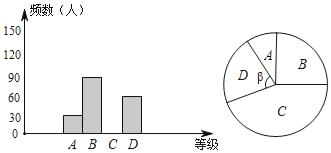
快乐小博士巩固与提高系列答案【题目】为了传承中华民族优秀传统文化,我县某中学组织了一次“中华民族优秀传统文化知识竞赛”活动,比赛后整理参赛学生的成绩,将参赛学生的成绩分为A、B、C、D四个等级,并制作了如下的统计表和统计图,但都不完整,请你根据统计图、表解答下列问题:
等级 | 频数(人) | 频率 |
A | 30 | 0.1 |
B | 90 | 0.3 |
C | m | 0.4 |
D | 60 | n |
(1)在表中,写出m;n的值.
(2)补全频数直方图;
(3)计算扇形统计图中圆心角β的度数.