题目内容
【题目】定义符号![]() 的含义为:当
的含义为:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 如:
如:![]() ,
,![]() =
=![]() 则
则![]() 的最大值是______.
的最大值是______.
【答案】![]()
【解析】
分析: 画出函数图象草图,利用函数图象的性质可得结论.
详解:在同一坐标系xOy中,画出函数二次函数y=-x2+1与正比例函数y=-x的图象,如图所示,
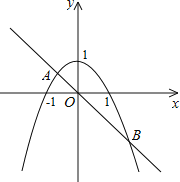
设它们交于点A、B,令-x2+1=-x,即x2-x-1=0,解得:x=![]() 或
或![]() ,
,
∴A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),观察图象可知:
),观察图象可知:
当x≤![]() 时,min{-x2+1,-x}=-x2+1,函数值随x的增大而增大,其最大值为
时,min{-x2+1,-x}=-x2+1,函数值随x的增大而增大,其最大值为![]() ,
,
当![]() <x≤
<x≤![]() 时,min{-x2+1,-x}=-x,函数值随x的增大而减小,没有最大值;
时,min{-x2+1,-x}=-x,函数值随x的增大而减小,没有最大值;
当x>![]() 时,min{-x2+1,-x}=-x2+1,函数值随x的增大而减小,最大值为
时,min{-x2+1,-x}=-x2+1,函数值随x的增大而减小,最大值为![]()
综上所示,min{-x2+1,-x}的最大值是![]() ,故答案为:
,故答案为:![]()
点睛: 本题考查了二次函数与正比例函数的图象与性质,充分理解定义min{a,b}和掌握函数的性质是解题的关键.

【题目】某校八年级根据学生的学习成绩、学习能力将学生依次分为A、B、C三个层次,第一次月考后,选取了其中一个A层次班级的考试成绩分布情况进行处理分析,制成频数分布表(成绩得分均为整数):
组别 | 成绩分组 | 频数 | 频率 |
1 | 39.5﹣49.5 | 2 | 0.05 |
2 | 49.5﹣59.5 | 4 | 0.10 |
3 | 59.5~69.5 | a | 0.20 |
4 | 69.5~79.5 | 10 | 0.25 |
5 | 79.5﹣89.5 | b | c |
6 | 89.5﹣100 | 6 | 0.15 |
合计 | 40 | 1.00 |
根据表中提供的信息解答下列各题:
(1)频数分布表中的a= ,b= ,c= ;
(2)将频数分布直方图补充完整;
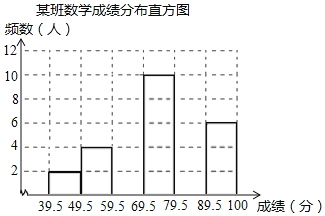
(3)小明正好在所选取的班级中,他认为:学校八年级共有20个班(平均每班40人),根据本班的成绩分布情况可知,在这次考试中,全年级90分以上为优秀,则优秀的人数约为 人,60分及以上为及格,及格的人数约为 人,及格的百分比约为 ;
(4)小明得到的数据会与实际情况相符吗?为什么?