题目内容
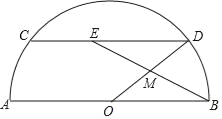
【题目】如图,半圆O的直径AB=20,弦CD∥AB,动点M在半径OD上,射线BM与弦CD相交于点E(点E与点C、D不重合),设OM=m.
(1)求DE的长(用含m的代数式表示);
(2)令弦CD所对的圆心角为α,且sin![]() .
.
①若△DEM的面积为S,求S关于m的函数关系式,并求出m的取值范围;
②若动点N在CD上,且CN=OM,射线BM与射线ON相交于点F,当∠OMF=90° 时,求DE的长.
【答案】(1)DE=![]() ;(2)①S=
;(2)①S=![]() ,(
,(![]() <m<10),②DE=
<m<10),②DE=![]() .
.
【解析】
(1)由CD∥AB知△DEM∽△OBM,可得![]() ,据此可得;
,据此可得;
(2)①连接OC、作OP⊥CD、MQ⊥CD,由OC=OD、OP⊥CD知∠DOP=![]() ∠COD,据此可得sin∠DOP=sin∠DMQ=
∠COD,据此可得sin∠DOP=sin∠DMQ=![]() 、sin∠ODP=
、sin∠ODP=![]() ,继而由OM=m、OD=10得QM=DMsin∠ODP=
,继而由OM=m、OD=10得QM=DMsin∠ODP=![]() (10﹣m),根据三角形的面积公式即可得;如图2,先求得PD=8、CD=16,证△CDM∽△BOM得
(10﹣m),根据三角形的面积公式即可得;如图2,先求得PD=8、CD=16,证△CDM∽△BOM得![]() ,求得OM=
,求得OM=![]() ,据此可得m的取值范围;
,据此可得m的取值范围;
②如图3,由BM=OBsin∠BOM=10×![]() =6,可得OM=8,根据(1)所求结果可得答案.
=6,可得OM=8,根据(1)所求结果可得答案.
(1)∵CD∥AB,
∴△DEM∽△OBM,
∴![]() ,即
,即![]() ,
,
∴DE=![]() ;
;
(2)①如图1,连接OC、作OP⊥CD于点P,作MQ⊥CD于点Q,
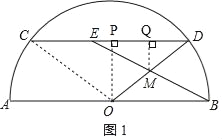
∵OC=OD、OP⊥CD,
∴∠DOP=![]() ∠COD,
∠COD,
∵sin![]() =
=![]() ,
,
∴sin∠DOP=sin∠DMQ=![]() ,sin∠ODP=
,sin∠ODP=![]() ,
,
∵OM=m、OD=10,
∴DM=10﹣m,
∴QM=DMsin∠ODP=![]() (10﹣m),
(10﹣m),
则S△DEM=![]() DEMQ=
DEMQ=![]() ×
×![]() ×
×![]() (10﹣m)=
(10﹣m)=![]() ,
,
如图2,
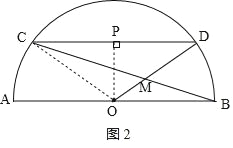
∵PD=ODsin∠DOP=10×![]() =8,
=8,
∴CD=16,
∵CD∥AB,
∴△CDM∽△BOM,
∴![]() ,即
,即![]() ,
,
解得:OM=![]() ,
,
∴![]() <m<10,
<m<10,
∴S=![]() ,(
,(![]() <m<10).
<m<10).
②当∠OMF=90°时,如图3,
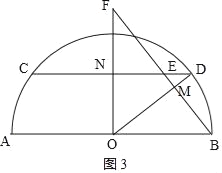
则∠BMO=90°,
在Rt△BOM中,BM=OBsin∠BOM=10×![]() =6,
=6,
则OM=8,
由(1)得DE=![]() .
.

 阅读快车系列答案
阅读快车系列答案