Question

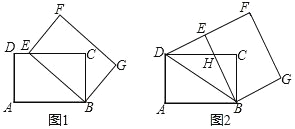
【题目】如图，在矩形 ABCD 中，AB＝5，AD＝3．以点 B 为中心，顺时针旋转矩形 BADC，得到矩形 BEFG，点 A、D、C 的对应点分别为 E、F、G．

（1）如图1，当点 E 落在 CD 边上时，求线段 CE 的长；

（2）如图2，当点 E 落在线段 DF 上时，求证：∠ABD＝∠EBD；

（3）在（2）的条件下，CD 与 BE 交于点 H，求线段 DH 的长．

Answer 1

【答案】（1）4；（2）见解析；（3）DH＝ ．

【解析】

（1）由旋转性质知BA＝BE＝5，由矩形性质知BC＝AD＝3，再在Rt△BCE中根据勾股定理可得；

（2）由旋转性质知∠BEF＝∠A＝90°，BE＝BA，结合点E落在线段DF得∠BED＝∠A＝90°，再利用“HL”证△ABD≌△EBD即可得；

（3）设DH＝x，从而得CH＝5﹣x，再由矩形的性质知∠ABD＝∠CDB，结合∠ABD＝∠EBD知∠CDB＝∠EBD，从而得DH＝BH＝x．在Rt△BCH中，根据CH2+BC2＝BH2求解可得．

（1）由旋转的性质知BA＝BE＝5．

∵四边形ABCD是矩形，∴AD＝BC＝3，∠C＝90°，∴CE4；

（2）由旋转的性质知∠BEF＝∠A＝90°，BE＝BA．

∵点E落在线段DF，∴∠BED＝∠A＝90°．

在△ABD和△EBD中，∵，∴△ABD≌△EBD（HL），∴∠ABD＝∠EBD；

（3）设DH＝x．

∵四边形ABCD是矩形，∴AB∥CD，AB＝CD＝5，∴CH＝CD﹣DH＝5﹣x，∠ABD＝∠CDB．

又∵∠ABD＝∠EBD，∴∠CDB＝∠EBD，∴DH＝BH＝x．在Rt△BCH中，∵CH2+BC2＝BH2，∴（5﹣x）2+32＝x2，解得：x，∴DH．