题目内容
【题目】如图,将边长为8的正方形纸片ABCD沿着EF折叠,使点C落在AB边的中点M处.点D落在点D'处,MD'与AD交于点G,则△AMG的内切圆半径的长为____________.
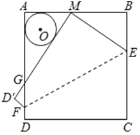
【答案】![]()
【解析】
由折叠求BE长,证明△AGM∽△BME,求AG长,进而由勾股定理求出MG长,根据内切圆的性质及三角形面积法解得内切圆半径长.
解:如图:
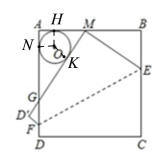
∵M是AB边中点,
∴AM=MB=4,
由折叠可得∠GME=∠C=90°,CE=ME,
设BE=x,由勾股定理可得x2+42=(8-x)2,
解得x=3,∴BE=3,
∵∠EMB+∠MEB=90°, ∠EMB+∠AMG=90°,
∴∠AMG=∠MEB,
∵∠A=∠B=90°,
∴△AGM∽△BME,
∴![]() ,即
,即![]() ,
,
∴AG=![]() ,
,
由勾股定理得,MG=![]() ,
,
∵⊙O为△AMG的内切圆,连接OH,ON,OK,
∴OH⊥AM,OH⊥AG, OK⊥GM,OH=ON=OK=r,
由△AMG面积可得,![]() ,
,
∴r=![]() .
.
故答案为:![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目