题目内容
【题目】如图，抛物线y＝ax2＋bx＋c经过△ABC的三个顶点，与y轴相交于(0， 
)，点A坐标为(－1，2)，点B是点A关于y轴的对称点，点C在x轴的正半轴上．
（1）求该抛物线的函数解析式；
（2）点F为线段AC上一动点，过点F作FE⊥x轴，FG⊥y轴，垂足分别为点E，G，当四边形OEFG为正方形时，求出点F的坐标；
（3）将（2）中的正方形OEFG沿OC向右平移，记平移中的正方形OEFG为正方形DEFG，当点E和点C重合时停止运动，设平移的距离为t，正方形的边EF与AC交于点M，DG所在的直线与AC交于点N，连接DM，是否存在这样的t，使△DMN是等腰三角形？若存在，求t的值；若不存在，请说明理由．
【答案】
（1）解：∵点B是点A关于y轴的对称点，
∴抛物线的对称轴为y轴，
∴抛物线的顶点为（0， 
），
故抛物线的解析式可设为y=ax2+ ．
∵A（﹣1，2）在抛物线y=ax2+ 上，
∴a+ =2，
解得a=﹣ 
，
∴抛物线的函数关系表达式为y=﹣ x2+
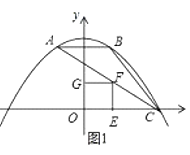
（2）解：①当点F在第一象限时，如图1，
令y=0得，﹣ x2+ =0，
解得：x1=3，x2=﹣3，
∴点C的坐标为（3，0）．
设直线AC的解析式为y=mx+n，
则有 
，
解得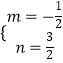 
，
∴直线AC的解析式为y=﹣ 
x+ 
．
设正方形OEFG的边长为p，则F（p，p）．
∵点F（p，p）在直线y=﹣ x+ 上，
∴﹣ p+ =p，
解得p=1，
∴点F的坐标为（1，1）．
②当点F在第二象限时，
同理可得：点F的坐标为（﹣3，3），
此时点F不在线段AC上，故舍去．
综上所述：点F的坐标为（1，1）
（3）解：过点M作MH⊥DN于H，如图2，
则OD=t，OE=t+1．
∵点E和点C重合时停止运动，∴0≤t≤2．
当x=t时，y=﹣ t+ ，则N（t，﹣ t+ ），DN=﹣ t+ ．
当x=t+1时，y=﹣ （t+1）+ =﹣ t+1，则M（t+1，﹣ t+1），ME=﹣ t+1．
在Rt△DEM中，DM2=12+（﹣ t+1）2= t2﹣t+2．
在Rt△NHM中，MH=1，NH=（﹣ t+ ）﹣（﹣ t+1）= ，
∴MN2=12+（ ）2= 
．
①当DN=DM时，
（﹣ t+ ）2= t2﹣t+2，
解得t= ；
②当ND=NM时，
﹣ t+ = 
，
解得t=3﹣ 
；
③当MN=MD时，
= t2﹣t+2，
解得t1=1，t2=3．
∵0≤t≤2，∴t=1．
综上所述：当△DMN是等腰三角形时，t的值为 ，3﹣ 或1．
【解析】（1）根据题意可知抛物线的对称轴是y轴以及顶点为（0，94），可设抛物线解析式为y=ax2+94，利用待定系数法将A点坐标代入求出a，进而可得到抛物线解析式。
（2）由于点F为AC上一动点，因此要对点F的位置分为①当点F在第一象限；②当点F在第二象限两种情况进行讨论。先根据题意可求出直线AC的函数解析式，再设OEFG的边长为p，则F（p，p），由于点F为AC上一点，那么只要将点F代入AC的解析式中即可求出点F的坐标，注意在求得F的坐标后要验证其是否在线段AC上。
（3）过点MH⊥DN于H，根据据题意可得0≤t≤2，然后只需用t的式子表示DN、DM2、MN2，分三种情况（①DN=DM，②ND=NM，③MN=MD）建立方程，解方程讨论就可求出△DMN是等腰三角形时t的值。
【考点精析】解答此题的关键在于理解因式分解法的相关知识，掌握已知未知先分离，因式分解是其次．调整系数等互反，和差积套恒等式．完全平方等常数，间接配方显优势，以及对确定一次函数的表达式的理解，了解确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法．
