��Ŀ����
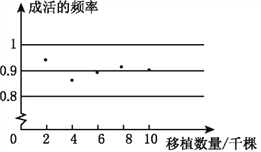
����Ŀ���������С����ܼ��ţ���̼���á����ߺ�ij���������豸�����IJ�Ʒ����Ӧ��������ҵ��ij�ֻ����豸ÿ�µIJ���������һ���ķ�Χ��ÿ�ײ�Ʒ�������ɱ�������44��Ԫ��ÿ�ײ�Ʒ���ۼ۲�����80��Ԫ����֪�����豸���²���x���ף���ÿ���ۼ�y1����Ԫ���������ϵʽy1=160��2x���²���x���ף��������ܳɱ�y2����Ԫ��������ͼ��ʾ�ĺ�����ϵ��
��1��ֱ��д��y2��x֮��ĺ�����ϵʽ��
��2�����²���x�ķ�Χ��
��3�����²���x���ף�Ϊ����ʱ�������豸������W����Ԫ�������������Ƕ��٣�
���𰸡�
��1���⣺��y2��x�ĺ�����ϵʽΪy2=kx+b��
![]() ����
���� ![]() ��
��
��y2��x֮��ĺ�����ϵʽ��y2=20x+600
��2���⣺������ɵã� ![]() ��
��
��ã�25��x��40��
���²���x��ȡֵ��Χ��25��x��34
��3���⣺������ɵã�
W=xy1��y2=x��160��20x����20x��600��
=��2��x��35��2+1850��
��25��x��40��
��x=35ʱ��Wȡ�����ֵ����ʱW=1850��
�����²���x���ף�Ϊ35��ʱ�����ֲ�Ʒ������W����Ԫ��������������2650��Ԫ
����������1���۲�ͼ��y2��x��һ�κ���������ͼ���ϵ��������꣬���������������ʽ��
��2���ҳ����еIJ��ȹ�ϵ��ÿ�ײ�Ʒ�������ɱ���44��Ԫ��ÿ�ײ�Ʒ���ۼۡ�80��Ԫ���г�����ʽ����⣬�������x��ȡֵ��Χ
��3�������W��x�ĺ�������ʽ������������꣬������������
�����㾫����ͨ���������һԪһ�β���ʽ��Ľⷨ��ȷ��һ�κ����ı���ʽ�����սⷨ���ٷֱ�����������ʽ���и�������ʽ�Ľ⼯�������������ʾ����������ʽ�Ľ⼯�����ҳ��������֣����ò���ʽ��ʾ���������ʽ��Ľ⼯�������Щ����ʽ�Ľ⼯��û�й������֣����������ʽ���� ( ��ʱҲ���������ʽ��Ľ⼯Ϊ�ռ� )��ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ���������Խ����⣮

 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�