题目内容
【题目】平面上，将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起，如图，则∠3+∠1﹣∠2= ．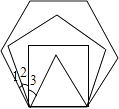 
【答案】24°
【解析】解：正三角形的每个内角是：
180°÷3=60°，
正方形的每个内角是：
360°÷4=90°，
正五边形的每个内角是：
（5﹣2）×180°÷5
=3×180°÷5
=540°÷5
=108°，
正六边形的每个内角是：
（6﹣2）×180°÷6
=4×180°÷6
=720°÷6
=120°，
则∠3+∠1﹣∠2
=（90°﹣60°）+（120°﹣108°）﹣（108°﹣90°）
=30°+12°﹣18°
=24°．
所以答案是：24°．
【考点精析】掌握多边形内角与外角和正多边形和圆是解答本题的根本，需要知道多边形的内角和定理：n边形的内角和等于（n-2）180°.多边形的外角和定理：任意多边形的外角和等于360°；圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角；圆的外切四边形的两组对边的和相等．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
