题目内容
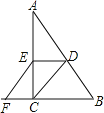
【题目】如图,将平行四边形ABCD折叠,使顶点D恰落在AB边上的点M处,折痕为AN,那么下列说法不正确的是( )

A. MN∥BCB. MN=AMC. AN=BCD. BM=CN
【答案】C
【解析】
根据平行四边形ABCD,可得∠B=∠D,再根据折叠可得∠D=∠NMA,再利用等量代换可得∠B=∠NMA,然后根据平行线的判定方法可得MN∥BC;首先证明四边形AMND是平行四边形,则BM=CN,AD=BC,再根据折叠可得AM=DA,则四边形AMND为菱形,再根据菱形的性质可得MN=AM.由以上可做出选择.
解:∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵根据折叠可得∠D=∠NMA,
∴∠B=∠NMA,
∴MN∥BC;故A正确;
∵四边形ABCD是平行四边形,
∴DN∥AM,AD∥BC,
∵MN∥BC,
∴AD∥MN,
∴四边形AMND是平行四边形,
∴BM=CN,AD=BC,
根据折叠可得AM=DA,
∴四边形AMND为菱形,
∴MN=AM;故B、D正确;
故选:C.

练习册系列答案
相关题目