题目内容
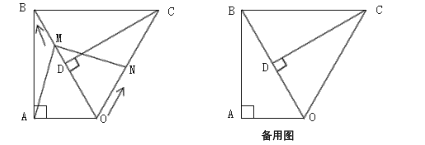
【题目】如图,已知![]() ,
,![]() ,
,![]() ,斜边
,斜边![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速行动,速度为
方向匀速行动,速度为![]() ;同时,点
;同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;当一个点停止运动,另一个点也停让运动.连接
;当一个点停止运动,另一个点也停让运动.连接![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() ,解答下列问题:
,解答下列问题:
(1)当![]() 为何值时,
为何值时,![]() 平分
平分![]() ?
?
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函教关系式;
的函教关系式;
(3)在运动过程中,当![]() 时,求四边形
时,求四边形![]() 的面积;
的面积;
(4)在运动过程中,是否存在某一时刻![]() ,使点
,使点![]() 为线段
为线段![]() 的中点?若存在,求出
的中点?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)存在,
;(4)存在,![]() ,理由见解析
,理由见解析
【解析】
(1)当![]() 平分
平分![]() 时,
时,![]() ≌
≌![]() ,得到AO=NO,继而问题得解;
,得到AO=NO,继而问题得解;
(2)由![]() ,进而求解;
,进而求解;
(3)关键当![]() 时,得到
时,得到![]() ,建立方程解得t的值继而求解;
,建立方程解得t的值继而求解;
(4)关键是过点C作CG//OB,得到![]() ∽
∽![]() ,有
,有![]() ,建立关于t的方程求解即可.
,建立关于t的方程求解即可.
解:(1)当![]() 平分
平分![]() 时,
时,
∵∠AMO=∠NMO,MO=MO,∠AOB=∠COD,
∴![]() ≌
≌![]() (ASA),
(ASA),
∴AO=NO,
∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴NO=AO=![]() ,
,
∴2t=4
∴![]()
(2)如图,![]() 分别为
分别为![]() 的边OM,ON上的高
的边OM,ON上的高
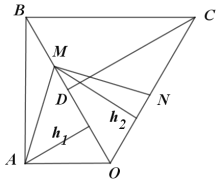
∵∠AOM=∠NOM=60°
∴![]() ,
,![]() ,
,
OM=4+t,ON=2t,
∴![]()
![]()
![]()
![]()
(3)由![]() 知,
知,![]()
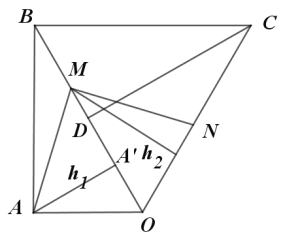
![]() ,MA
,MA![]() =OM-DA
=OM-DA![]() ,而OA
,而OA![]() =cos60°×AO=2
=cos60°×AO=2
∴![]()
∴![]()
∴![]()
∴![]()
(4)存在,理由如下
如图过点C作CG//OB,交MN的延长线于点G ,
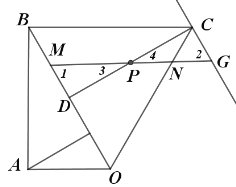
∴∠1=∠2,∠3=∠4,PD=PC
![]() ≌
≌![]()
∴MD=CG=t,
由CG//OB,易知![]() ∽
∽![]()
又∵![]() ,
,
而ON=2t,CN=8-2t,OM=OD+DM=4+t,
∴![]()
解得:![]() ,
,
经检验,![]() 是原方程的解,
是原方程的解,
故存在某一时刻![]() ,使点
,使点![]() 为线段
为线段![]() 的中点.
的中点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目