题目内容
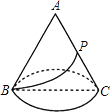
【题目】如图,圆锥的轴截面是边长为6cm的正三角形ABC,P是母线AC的中点.则在圆锥的侧面上从B点到P点的最短路线的长为_____.
【答案】3![]() .
.
【解析】
求出圆锥底面圆的周长,则以AB为一边,将圆锥展开,就得到一个以A为圆心,以AB为半径的扇形,根据弧长公式求出展开后扇形的圆心角,求出展开后∠BAC=90°,连接BP,根据勾股定理求出BP即可.
解:圆锥底面是以BC为直径的圆,圆的周长是BCπ=6π,
以AB为一边,将圆锥展开,就得到一个以A为圆心,以AB为半径的扇形,弧长是l=6π,
设展开后的圆心角是n°,则![]() ,
,
解得:n=180,
即展开后∠BAC=![]() ×180°=90°,
×180°=90°,
AP=![]() AC=3,AB=6,
AC=3,AB=6,
则在圆锥的侧面上从B点到P点的最短路线的长就是展开后线段BP的长,
由勾股定理得:BP=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目