题目内容
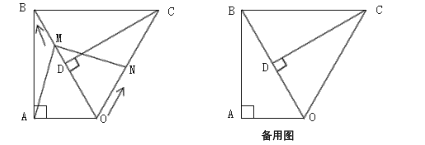
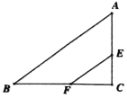
【题目】如图，已知Rt△ABC中，∠C=90°，AC=6，BC=8，点E、F分别是边AC、BC上的动点,且EF//AB，点C关于EF的对称点D恰好落在△ABC的内角平分线上，则CD长为__________．
【答案】3或
【解析】
点C关于EF的对称点D恰好落在△ABC的内角平分线上，有两种情况：∠ABC或∠ACB的角平分线；正确画出图形，得出点D即角平分线与AB边高CH的交点，再由角平分线性质可得DH=DG=CH-CD，点C关于EF的对称点D恰好落在∠ABC的角平分线上，利用
列方程即可求出CD．
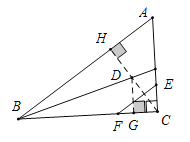
解：i、当点C关于EF的对称点D恰好落在∠ABC的角平分线上时，
过C点作CH⊥EF，交AB于点H，交∠ABC平分线与点D，
∵点C关于EF的对称点D恰好落在∠ABC的内角平分线上，故点D即点C关于EF的对称点，
∵∠C=90°，AC=6，BC=8，
∴
，
∴
，
∵CH⊥EF，EF//AB,
∴CH⊥AB，
∴
， ∠BCH=∠A，
过D点作DG⊥BC，垂足为G，
∵DB平分∠ABC，DH⊥AB，DG⊥BC，
∴DH=DG=CH-CD，
∵
，
，
∴
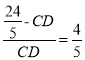，解得： 
；
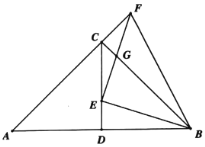
ii、当点C关于EF的对称点D恰好落在∠BAC的角平分线上时，如图，
同理可得：
，
综上所述：点C关于EF的对称点D恰好落在△ABC的内角平分线上，则CD长为3或．
故答案为：3或．
练习册系列答案
相关题目
