Question

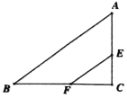
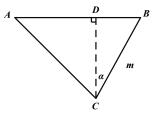
【题目】如图，在△ABC中，∠ACB=90°，AC=BC，CD是AB边上的中线，点E为线段CD上一点（不与点C、D重合），连接BE，作EF⊥BE与AC的延长线交于点F，与BC交于点G，连接BF．

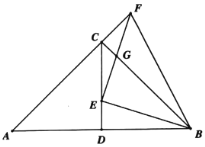
（1）求证：△CFG∽△EBG；

（2）求∠EFB的度数；

（3）求的值；

Answer 1

【答案】（1）证明见解析；（2）45°，（3）

【解析】

（1）得出∠FCG=∠BEG=90°，∠CGF=∠EGB，则结论得证；
（2）证明△CGE∽△FGB，得出∠EFB=∠ECG=∠ACB=45°；
（3）过点F作FH⊥CD交DC的延长线于点H，证明△FEH≌△EBD（AAS），得出FH=ED，则CH=FH，得出CF=DE，则得出答案．

（1）证明：∵，，

∴，

又∵，

∴．

（2）解：由（1）得，

∴，∴，

又∵,

∴，

∴．

（3）解：过点F作FH⊥CD交DC的延长线于点H，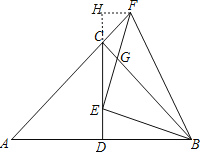

由（2）知，△BEF是等腰直角三角形，
∴EF=BE，
∵∠FEH+∠DEB=90°，∠EBD+∠DEB=90°，
∴∠FEH=∠EBD，
在△FEH和△EBD中，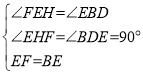
，
∴△FEH≌△EBD（AAS），
∴FH=ED，
∵∠FCH=∠ACD=45°，∠CHF=90°，
∴∠CFH=∠CFH=45°，
∴CH=FH，
在Rt△CFH中，CF=FH，
∴CF=DE，
∴．