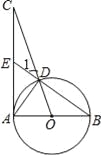
题目内容
【题目】如图,AB是⊙O的弦,点C为半径OA的中点,过点C作CD⊥OA交弦AB于点E,连接BD,且DE=DB.
(1)判断BD与⊙O的位置关系,并说明理由;
(2)若CD=15,BE=10,tanA=![]() ,求⊙O的直径.
,求⊙O的直径.
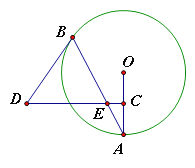
【答案】(1)BD是⊙O的切线,理由见解析;(2)![]() .
.
【解析】试题分析:(1)连接OB,由已知条件易证∠OBD=90°,即可证明BD是⊙O的切线;(2)过点D作DG⊥BE于G,根据等腰三角形的性质得到EG=![]() BE=5,由两角相等的三角形相似,△ACE∽△DGE,利用相似三角形对应角相等得到sin∠EDG=sinA=
BE=5,由两角相等的三角形相似,△ACE∽△DGE,利用相似三角形对应角相等得到sin∠EDG=sinA=![]() ,在Rt△EDG中,利用勾股定理求出DG的长,根据三角形相似得到比例式,代入数据即可得到结果.
,在Rt△EDG中,利用勾股定理求出DG的长,根据三角形相似得到比例式,代入数据即可得到结果.
试题解析:(1)证明:连接OB,
∵OB=OA,DE=DB,
∴∠A=∠OBA,∠DEB=∠ABD,
又∵CD⊥OA,
∴∠A+∠AEC=∠A+∠DEB=90°,
∴∠OBA+∠ABD=90°,
∴OB⊥BD,
∴BD是⊙O的切线;
(2)如图,过点D作DG⊥BE于G,
∵DE=DB,
∴EG=![]() BE=5,
BE=5,
∵∠ACE=∠DGE=90°,∠AEC=∠GED,
∴∠GDE=∠A,
∴△ACE∽△DGE,
∴sin∠EDG=sinA=![]() =
=![]() ,即CE=13,
,即CE=13,
在Rt△ECG中,
∵DG=![]() =12,
=12,
∵CD=15,DE=13,
∴DE=2,
∵△ACE∽△DGE,
∴![]() =
=![]() ,
,
∴AC=![]() DG=
DG=![]() ,
,
∴⊙O的直径2OA=4AD=![]() .
.


练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目