题目内容
【题目】如图，一次函数y=－
x＋3的图像分别与x轴、y轴交于A、B两点．动点P从A点开始沿折线AO－OB－BA运动，点P在AO，OB，BA上运动的速度分别为1，，2 (长度单位/秒)；动点E从O点开始以
(长度单位/秒)的速度沿线段OB运动．设P、E两点同时出发，运动时间为t (秒)，当点P沿折线AO－OB－BA运动一周时，动点E和P同时停止运动．过点E作EF∥OA，交AB于点F．
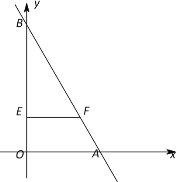
（1）求线段AB的长；
（2）求证：∠ABO=30°；
（3）当t为何值时，点P与点E重合?
（4）当t = 时，PE=PF ．
【答案】（1）6；（2）详见解析；（3）
；（4）
【解析】
（1）令y=0，求出x，得出A的坐标及OA的长，令x=0，得出B的坐标及OB的长，利用勾股定理即可求出AB的长；
（2）取AB的中点C，连接OC．证明△OAC是等边三角形，得到∠OAB=60°．根据三角形内角和定理即可得出结论；
（3）由于P在OB上与E重合，则E的路程为OE，E所用的时间为t秒，P的路程为OA+OE，P在OA上所用的时间为3秒，在OE上所用的时间为（t-3）秒，根据P在OB上的路程与E的路程相同列方程，求解即可；
（4）先求出点P沿折线AO－OB－BA运动一周时所花的时间为9秒．然后分三种情况讨论：①当P在线段AO上时；②当P在线段OB上时；③当P在线段BA上时．
（1）令y=0，得：y=－
x＋3=0，解得：x=3，∴A（3，0），∴OA=3．
令x=0，得：y=3，∴B（0，
），∴OB=．
∵∠AOB=90°，∴AB=
=6；
（2）取AB的中点C，连接OC．
∵∠AOB=90°，C为AB的中点，∴OC=BC=CA=3．
∵OA=3，∴OC=CA=OA，∴△OAC是等边三角形，∴∠OAB=60°．
∵∠AOB=90°，∴∠ABO=30°；
（3）由题意得：
，解得：
，所以当时，点P与点E重合．
（4）P从A到O的时间为t=3÷1=3（秒），P从O到B的时间为÷ =3（秒），P从B到A的时间为：6÷2=3（秒），故点P沿折线AO－OB－BA运动一周时所花的时间为3+3+3=9（秒）．分三种情况讨论：
①当P在线段AO上时，即0＜t＜3时，由题意知：P（3-t，0），E（0，
）．设F（a，b）．
∵EF∥OA，∴b=．
∵F在直线AB上，∴
，解得：a=
．∴F（，）．
∵PE=PF，∴P在EF的垂直平分线上，∴2（3-t）=，解得：t=
；
②当P在线段OB上时，即3≤t＜6时，由题意知：P（0，
），E（0，），F（，）．
∵PE=PF，∴|－|=
，∴=0，解得：t=9（舍去）；
③当P在线段BA上时，即6≤t＜9时，由题意知：E（0，），F（，），BP= 
．设P（m，n），则m=
BP=
．
∵PE=PF，∴P在EF的垂直平分线上，∴2（t-6）=，解得：t=
．
综上所述：t=或．
