��Ŀ����
�׳�����·��ɲ�����飬�ռ������������±���ʾ��
�ٶ� (ǧ��/ʱ) (ǧ��/ʱ) | 0 | 5 | 10 | 15 | 20 | 25 | �� |
ɲ������ (��) (��) | 0 |  | 2 |  | 6 |  | �� |
 ��Ϊ������꣬����ͼ��ʾ������ϵ�л���ɲ������
��Ϊ������꣬����ͼ��ʾ������ϵ�л���ɲ������ (��)���ٶ�
(��)���ٶ� (ǧ��/ʱ)�ĺ���ͼ�������Ľ���ʽ��
(ǧ��/ʱ)�ĺ���ͼ�������Ľ���ʽ��
(2)��һ������Ϊ40ǧ��/ʱ����·�ϣ��ס�������������У�ͬʱɲ������������ײ�ˣ��º��üס�������ɲ������ֱ�Ϊ12��10.5�ף���֪�ҳ�ɲ������
 (��)���ٶ�
(��)���ٶ� (ǧ��/ʱ)���㺯��
(ǧ��/ʱ)���㺯�� ������������ٶȷ��������ײԭ��
������������ٶȷ��������ײԭ��
������
���������������1����������ٰ��Ա�����С�����˳������.��ͼ��֪��������,�躯������ʽΪy=ax2+bx+c�ô���ϵ������������뼴�����a,b,c.�Ӷ���ý���ʽ��2���ס�������ɲ������ֱ�Ϊ12��10.5�ף�������ֵ,�ֱ����y=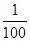 x2+
x2+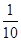 x��
x�� ,����ٶ�
,����ٶ� (ǧ��/ʱ)������Ϊ40ǧ��/ʱ�ȽϷ�����ײԭ��.
(ǧ��/ʱ)������Ϊ40ǧ��/ʱ�ȽϷ�����ײԭ��.
�����������1��ͼ���ͼ
�躯������ʽΪy=ax2+bx+c��
�ѣ�0��0������10��2������20��6�����룬�ã� ���
���
��y=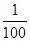 x2+
x2+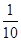 x��
x��
��2����y=12ʱ����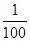 x2+
x2+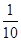 x=12�����x1=��40����ȥ����x2=30��
x=12�����x1=��40����ȥ����x2=30��
��y��=10.5ʱ��10.5=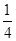 x�����x=42��
x�����x=42��
���ҳ���ʻ�ٶ��ѳ�������40ǧ��/ʱ���ٶ�̫�죬ײ����������ʻ�ļ׳���
���㣺1.����ϵ������������ʽ.2�к���ֵ���Ա�����ֵ.

��ϰ��ϵ�д�
�����Ŀ
 ��ͬһֱ��
��ͬһֱ�� �ϣ��ҵ�
�ϣ��ҵ� ���
��� �غϡ��̶ֹ�
�غϡ��̶ֹ� ����
���� ��ÿ��1����λ���ȵ��ٶ���
��ÿ��1����λ���ȵ��ٶ��� ���
��� �غ�ʱ�˶�ֹͣ����ƽ��ʱ��Ϊ
�غ�ʱ�˶�ֹͣ����ƽ��ʱ��Ϊ �롣
�롣
 ��ǡ�þ�����
��ǡ�þ����� ����
���� ����ֱ��д��
����ֱ��д�� Ϊ�߶�
Ϊ�߶� ��һ�㣬��һ����
��һ�㣬��һ���� �ӵ�
�ӵ� �����˶��������
�����˶�������� �����˶������
�����˶������

 ����ƽ��
����ƽ��
 ����λ���ȣ�ʹ֮����
����λ���ȣ�ʹ֮���� ����
���� ��ֵ��
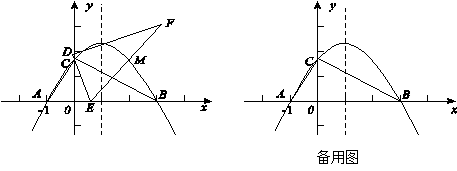
��ֵ�� ��x�ύ���A(1,0)���B, �ҹ���C(0��3)��
��x�ύ���A(1,0)���B, �ҹ���C(0��3)��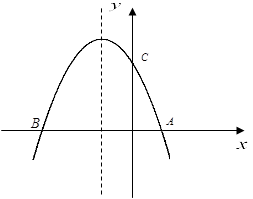
 ��ֱ��
��ֱ�� ���ڵ�
���ڵ� ����
���� ����������
���������� ��
�� ֮���һ�����㣬����
֮���һ�����㣬���� �ᡢ
�ᡢ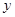 ���ƽ������ֱ��
���ƽ������ֱ�� ���ڵ�
���ڵ� ��
�� ��
��
 �ij���
�ij��� Ϊ�߹������
Ϊ�߹������ �����
����� ������Ϊ
������Ϊ �����
����� ֮��Ĺ�ϵʽ��
֮��Ĺ�ϵʽ��

 �У���OΪԭ�㣬��B�ڷ���������
�У���OΪԭ�㣬��B�ڷ��������� ��
�� ��
�� ��ͼ���ϣ���BOC�����Ϊ
��ͼ���ϣ���BOC�����Ϊ ��
��
 ����λ���ٶ��˶���������һ�����㵽��˵�ʱ����һ��������ֹ֮ͣ�˶������˶�ʱ����t��ʾ����BEF�������
����λ���ٶ��˶���������һ�����㵽��˵�ʱ����һ��������ֹ֮ͣ�˶������˶�ʱ����t��ʾ����BEF������� ��ʾ�����S����t�ĺ�����ϵʽ����������˶�ʱ��tȡ��ֵʱ����BEF��������
��ʾ�����S����t�ĺ�����ϵʽ����������˶�ʱ��tȡ��ֵʱ����BEF��������  ��ʱ�������������Ƿ���ڵ�P��ʹ��PEF���ܳ���С�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��ʱ�������������Ƿ���ڵ�P��ʹ��PEF���ܳ���С�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�