��Ŀ����
������ֱ�������Σ��ڡ�ABC�У���ACB=90�㣬AC=3��BC=6���ڡ�DEF�У���FDE=90�㣬DE=DF=4����������ֱ�������ΰ�ͼ1��ʾλ�ðڷţ�����ֱ�DZ� ��ͬһֱ��
��ͬһֱ�� �ϣ��ҵ�
�ϣ��ҵ� ���
��� �غϡ��̶ֹ�
�غϡ��̶ֹ� ����
���� ��ÿ��1����λ���ȵ��ٶ���
��ÿ��1����λ���ȵ��ٶ��� ������ƽ�ƣ�����
������ƽ�ƣ����� ���
��� �غ�ʱ�˶�ֹͣ����ƽ��ʱ��Ϊ
�غ�ʱ�˶�ֹͣ����ƽ��ʱ��Ϊ �롣
�롣
��1���� Ϊ ��ʱ��
Ϊ ��ʱ�� ��ǡ�þ�����
��ǡ�þ����� ����
���� Ϊ ��ʱ���˶�ֹͣ��
Ϊ ��ʱ���˶�ֹͣ��
��2���� ƽ�ƹ����У���
ƽ�ƹ����У��� ��
�� �ص����ֵ����Ϊ
�ص����ֵ����Ϊ ����ֱ��д��
����ֱ��д�� ��
�� �ĺ�����ϵʽ����д��
�ĺ�����ϵʽ����д�� ��ȡֵ��Χ��
��ȡֵ��Χ��
��3���� ֹͣ�˶�����ͼ2��
ֹͣ�˶�����ͼ2�� Ϊ�߶�
Ϊ�߶� ��һ�㣬��һ����
��һ�㣬��һ����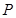 �ӵ�
�ӵ� ����������
���������� �����˶��������
�����˶�������� ������б��
������б�� �����˶������
�����˶������ �����ö���
�����ö���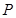 ���߶�
���߶� ���˶����ٶ�������б��
���˶����ٶ�������б�� ���˶��ٶȵ�2������ȷ��б��
���˶��ٶȵ�2������ȷ��б�� ���¶ȣ�ʹ�øö���ӵ�
���¶ȣ�ʹ�øö���ӵ� �˶�����
�˶����� ���õ�ʱ����̡���Ҫ����ȷ����
���õ�ʱ����̡���Ҫ����ȷ���� λ�õķ���������Ҫ��֤������
λ�õķ���������Ҫ��֤������
��1��2��7����2����0��t��2ʱ��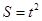 ����2��t��3ʱ��
����2��t��3ʱ��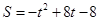 ��3��t��4ʱ��
��3��t��4ʱ��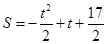 ����4��t��7ʱ��
����4��t��7ʱ��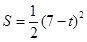 ����3��
����3��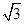 .
.
�������������(1)��E��EH��AB��������H����AHΪAB���ƶ��ľ��룬���á�AHE�ס�CAB�����AH�ij����������AB���˶�ʱ�䣻��C��F�غ�ʱ��C���˶���·ΪCF���������ʱ��t��
��2���������������ε�֪ʶ�ɷ�ʱ������S��t֮��ĺ�����ϵʽ.
��3����l���·�����DAM=30�㣬�ٹ���E��EN��AM��N����AD��G����ʱ�˶�ʱ����̣�i=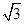 .
.
�����������1���� Ϊ 2 ��ʱ��
Ϊ 2 ��ʱ�� ��ǡ�þ�����
��ǡ�þ����� ����
���� Ϊ 7 ��ʱ���˶�ֹͣ��
Ϊ 7 ��ʱ���˶�ֹͣ��
��2����0��t��2ʱ��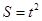 ����2��t��3ʱ��
����2��t��3ʱ��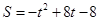 ��3��t��4ʱ��
��3��t��4ʱ��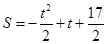 ����4��t��7ʱ��
����4��t��7ʱ��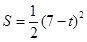 ��
��
��3����l���·�����DAM=30�㣬�ٹ���E��EN��AM��N����AD��G����ʱ�˶�ʱ����̣�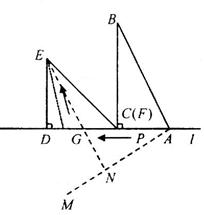
���AGN=60��
���EGD=60��
��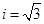
����: ��1�����κ�������2���¶�.

�׳�����·��ɲ�����飬�ռ������������±���ʾ��
�ٶ� (ǧ��/ʱ) (ǧ��/ʱ) | 0 | 5 | 10 | 15 | 20 | 25 | �� |
ɲ������ (��) (��) | 0 |  | 2 |  | 6 |  | �� |
 ��Ϊ������꣬����ͼ��ʾ������ϵ�л���ɲ������
��Ϊ������꣬����ͼ��ʾ������ϵ�л���ɲ������ (��)���ٶ�
(��)���ٶ� (ǧ��/ʱ)�ĺ���ͼ�������Ľ���ʽ��
(ǧ��/ʱ)�ĺ���ͼ�������Ľ���ʽ��
(2)��һ������Ϊ40ǧ��/ʱ����·�ϣ��ס�������������У�ͬʱɲ������������ײ�ˣ��º��üס�������ɲ������ֱ�Ϊ12��10.5�ף���֪�ҳ�ɲ������
 (��)���ٶ�
(��)���ٶ� (ǧ��/ʱ)���㺯��
(ǧ��/ʱ)���㺯�� ������������ٶȷ��������ײԭ��
������������ٶȷ��������ײԭ�� 
 ���������ϵ�һ�㣬���ABD�������
���������ϵ�һ�㣬���ABD�������
 ����A����3��0����B��1��0�����㣬��y�ύ�ڵ�C���䶥��ΪD���Գ�����ֱ��l��l��x�ύ�ڵ�H��
����A����3��0����B��1��0�����㣬��y�ύ�ڵ�C���䶥��ΪD���Գ�����ֱ��l��l��x�ύ�ڵ�H��

 ��ͼ��ԭ�㼰��A��1��2������x���ཻ����һ��B��
��ͼ��ԭ�㼰��A��1��2������x���ཻ����һ��B��
 �Ľ���ʽ��B�����ꣻ
�Ľ���ʽ��B�����ꣻ Ϊ�Գ������ҷ��ۺõ�һ���µĶ��κ���
Ϊ�Գ������ҷ��ۺõ�һ���µĶ��κ��� ����֪���κ���
����֪���κ���