题目内容
如图,抛物线y=ax2+bx(a>0)经过原点O和点A(2,0).
(1)写出抛物线的对称轴与x轴的交点坐标;
(2)点(x1,y1),(x2,y2)在抛物线上,若x1<x2<1,比较y1,y2的大小;
(3)点B(﹣1,2)在该抛物线上,点C与点B关于抛物线的对称轴对称,求直线AC的函数关系式.
(1)(1,0);(2)y1>y2;(3)y=2x﹣4.
解析试题分析:(1)根据图示可以直接写出抛物线的对称轴与x轴的交点坐标;(2)根据抛物线的对称轴与x轴的交点坐标可以求得该抛物线的对称轴是x=1,然后根据函数图象的增减性进行解题;(3)根据已知条件可以求得点C的坐标是(3,2),所以根据点A、C的坐标来求直线AC的函数关系式.
试题解析:(1)根据图示,由抛物线的对称性可知,抛物线的对称轴与x轴的交点坐标(1,0).
(2)抛物线的对称轴是直线x=1.
根据图示知,当x<1时,y随x的增大而减小,∴当x1<x2<1时,y1>y2.
(3)∵对称轴是x=1,点B(﹣1,2)在该抛物线上,点C与点B关于抛物线的对称轴对称,
∴点C的坐标是(3,2).
设直线AC的关系式为y=kx+b(k≠0),则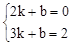 ,解得
,解得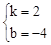 .
.
∴直线AC的函数关系式是:y=2x﹣4.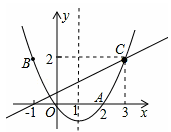
考点:1.抛物线与x轴的交点;2.待定系数法的应用;3.曲线上点的坐标与方程的关系;4.二次函数的性质;5.轴对称的性质.

练习册系列答案
相关题目
甲车在弯路做刹车试验,收集到的数据如下表所示:
速度 (千米/时) (千米/时) | 0 | 5 | 10 | 15 | 20 | 25 | … |
刹车距离 (米) (米) | 0 |  | 2 |  | 6 |  | … |
 作为点的坐标,在如图所示的坐标系中画出刹车距离
作为点的坐标,在如图所示的坐标系中画出刹车距离 (米)与速度
(米)与速度 (千米/时)的函数图象,并求函数的解析式;
(千米/时)的函数图象,并求函数的解析式;
(2)在一个限速为40千米/时的弯路上,甲、乙两车相向而行,同时刹车,但还是相撞了.事后测得甲、乙两车刹车距离分别为12米和10.5米,又知乙车刹车距离
 (米)与速度
(米)与速度 (千米/时)满足函数
(千米/时)满足函数 ,请你就两车速度方面分析相撞原因.
,请你就两车速度方面分析相撞原因. 
 的一元二次方程
的一元二次方程 有实数根,
有实数根,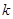 为正整数.
为正整数. 的图象向下平移8个单位,求平移后的图象的解析式;
的图象向下平移8个单位,求平移后的图象的解析式;