题目内容
矩形纸片ABCD中,AB=5,AD=4.
(1)如图1,四边形MNEF是在矩形纸片ABCD中裁剪出的一个正方形.你能否在该矩形中裁剪出一个面积最大的正方形,最大面积是多少?说明理由;
(2)请用矩形纸片ABCD剪拼成一个面积最大的正方形.要求:在图2的矩形ABCD中画出裁剪线,并在网格中画出用裁剪出的纸片拼成的正方形示意图(使正方形的顶点都在网格的格点上).
解:(1)正方形的最大面积是16。理由如下:设AM=x(0≤x≤4),则MD=4﹣x。
∵四边形MNEF是正方形,∴MN=MF,∠AMN+∠FMD=90°。
∵∠AMN+∠ANM=90°,∴∠ANM=∠FMD。
∵在△ANM和△DMF中, ,∴△ANM≌△DMF(AAS)。∴DM=AN。
,∴△ANM≌△DMF(AAS)。∴DM=AN。
∴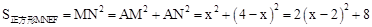 。
。
∵函数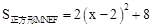 的开口向上,对称轴是x=2,
的开口向上,对称轴是x=2,
∴在对称轴的左侧S随x的增大而减小,在对称轴的右侧S随x的增大而增大。
∵0≤x≤4,∴当x=0或x=4时,正方形MNEF的面积最大,最大值是16。
(2)先将矩形纸片ABCD分割成4个全等的直角三角形和两个矩形如图1,然后拼成如图2的正方形。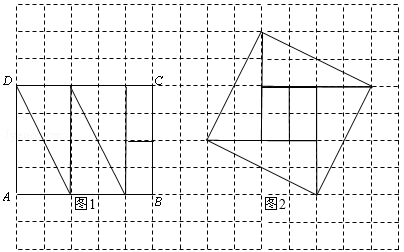
解析试题分析:(1)设AM=x(0≤x≤4)则MD=4﹣x,根据正方形的性质就可以得出Rt△ANM≌Rt△DMF.根据正方形的面积就可以表示出解析式,由二次函数的性质就可以求出其最值。
(2)先将矩形纸片分割成4个全等的直角三角形和两个矩形如图,根据赵爽弦图的构图方法就可以拼成正方形。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
甲车在弯路做刹车试验,收集到的数据如下表所示:
速度 (千米/时) (千米/时) | 0 | 5 | 10 | 15 | 20 | 25 | … |
刹车距离 (米) (米) | 0 |  | 2 |  | 6 |  | … |
 作为点的坐标,在如图所示的坐标系中画出刹车距离
作为点的坐标,在如图所示的坐标系中画出刹车距离 (米)与速度
(米)与速度 (千米/时)的函数图象,并求函数的解析式;
(千米/时)的函数图象,并求函数的解析式;
(2)在一个限速为40千米/时的弯路上,甲、乙两车相向而行,同时刹车,但还是相撞了.事后测得甲、乙两车刹车距离分别为12米和10.5米,又知乙车刹车距离
 (米)与速度
(米)与速度 (千米/时)满足函数
(千米/时)满足函数 ,请你就两车速度方面分析相撞原因.
,请你就两车速度方面分析相撞原因.  .
.
 (b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由. 与直线
与直线 交于点O(0,0),
交于点O(0,0), 。点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E。
。点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E。

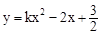 (
( 是常数)
是常数) 轴只有一个交点,求
轴只有一个交点,求 在某反比例函数的图像上,要使该反比例函数和二次函数
在某反比例函数的图像上,要使该反比例函数和二次函数 随
随 两点,且
两点,且 ,
, ,在
,在