Question

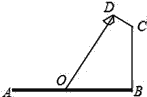
【题目】如图，在Rt△ABC中，∠ACB＝90°，AC＝1，tan∠CAB＝2，将△ABC绕点A旋转后，点B落在AC的延长线上的点D，点C落在点E，DE与直线BC相交于点F，那么CF＝_____．

Answer 1

【答案】.

【解析】

根据已知条件得到BC＝ACtan∠CAB＝2，根据勾股定理得到AB＝，根据旋转的性质得到AD＝AB＝，∠D＝∠B，根据三角函数的定义即可得到结论．

如图，

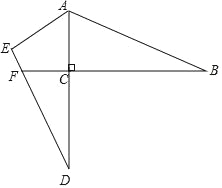
∵在Rt△ABC中，∠ACB＝90°，AC＝1，tan∠CAB＝2，

∴BC＝ACtan∠CAB＝2，

∴AB＝，

∵将△ABC绕点A旋转后，点B落在AC的延长线上的点D，

∴AD＝AB＝，∠D＝∠B，

∵AC＝1，

∴CD＝﹣1，

∵∠FCD＝∠ACB＝90°，

∴tanD＝tan∠CAB＝＝2，

∴CF＝，

故答案为：．