题目内容
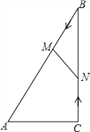
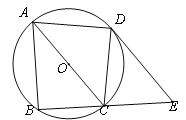
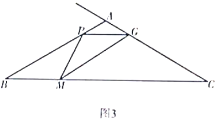
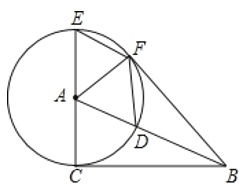
【题目】如图,在![]() 中,
中,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作
的长为半径作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .过点
.过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)填空:
①当四边形![]() 是周长为20的菱形时,
是周长为20的菱形时,![]() ;
;
②当![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
【答案】(1)见详解;(2)①![]() ,②
,②![]() .
.
【解析】
(1)根据平行线的性质得∠E=∠CAB,∠EFA=∠FAB,由于∠E=∠EFA,则∠FAB=∠CAB,可证明△ABC≌△ABF,从而得到∠AFB=90°,然后根据切线的判定方法可判断BF是⊙A的切线;
(2)①通过菱形得到△ADF为等边三角形,然后通过特殊角的三角函数值计算即可;②由正方形对角线和边的倍数关系即可得到答案.
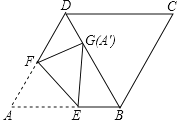
(1)证明:∵EF∥AB,
∴∠E=∠CAB,∠EFA=∠FAB,
∵AE=AF,
∴∠E=∠EFA,
∴∠FAB=∠CAB,
在△ABC和△ABF中,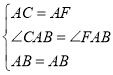 ,
,
∴△ABC≌△ABF(SAS),
∴∠AFB=∠ACB=90°,
∴BF⊥AF,
∵AF是⊙A的半径,
∴BF是⊙A的切线;
(2)①若四边形![]() 是周长为20的菱形,
是周长为20的菱形,
则AD=DF=5,
∵AD=AF
∴AD=AF=DF=5,即△ADF为等边三角形,
∴∠DAF=60°,
∵∠AFB=90°,
∴![]() ,
,
∴![]() ;
;
②若四边形![]() 是正方形,
是正方形,
则AB是正方形的对角线,
由于AE=AC=AF,
∴![]() .
.

【题目】为了从小华和小亮两人中选拔一人参加射击比赛,现对他们的射击水平进行测试,两人在相同条件下各射击6次,命中的环数如下(单位:环):
小华:7,8,7,8,9,9; 小亮:5,8,7,8,10,10.
(1)填写下表:
平均数(环) | 中位数(环) | 方差(环2) | |
小华 | 8 | ||
小亮 | 8 | 3 |
(2)根据以上信息,你认为教练会选择谁参加比赛,理由是什么?
(3)若小亮再射击2次,分别命中7环和9环,则小亮这8次射击成绩的方差 .(填“变大”、“变小”、“不变”)