题目内容
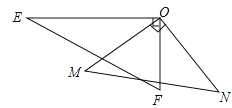
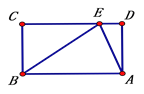
【题目】如图,已知点A,C在EF上,AD∥BC,DE∥BF,AE=CF.
(1)求证:四边形ABCD是平行四边形;
(2)直接写出图中所有相等的线段(AE=CF除外).

【答案】(1)见解析;(2)AD=BC,EC=AF,ED=BF,AB=DC.
【解析】整体分析:
(1)用ASA证明△ADE≌△CBF,得到AD=BC,根据一组对边平行且相等的四边形是平行四边形证明;(2)根据△ADE≌△CBF,和平行四边形ABCD的性质及线段的和差关系找相等的线段.
解:(1)证明:∵AD∥BC,DE∥BF,
∴∠E=∠F,∠DAC=∠BCA,∴∠DAE=∠BCF.
在△ADE和△CBF中,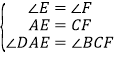 ,
,
∴△ADE≌△CBF,∴AD=BC,
∴四边形ABCD是平行四边形.
(2)AD=BC,EC=AF,ED=BF,AB=DC.
理由如下:
∵△ADE≌△CBF,∴AD=BC,ED=BF.
∵AE=CF,∴EC=AF.
∵四边形ABCD是平行四边形,∴AB=DC.

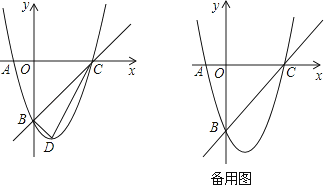
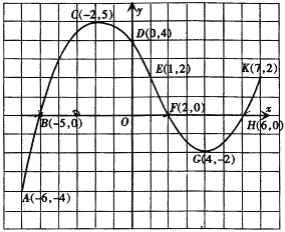
【题目】大家知道,函数图象特征与函数性质之间存在着必然联系.请根据图中的函数图象特征及表中的提示,说出此函数的变化规律.此外,你还能说出此函数的哪些性质?
序号 | 函数图象特征 | 函数变化规律 |
(1) | 曲线从点A(-6,-4)至点K(7,2) | 自变量的取值范围是______. |
(2) | 曲线与y轴交于点D(0,4) | 当x=______时,y=______. |
(3) | 曲线与x轴分别交于点B(-5,0)、F(2,0)、H(6,0) | 当x的值分别为______时,y=0. |
(4) | 曲线经过点E(1,2) | 当x=______时,y=______. |
(5) | 由左至右曲线AC呈上升状态 | 当-6≤x≤-2时,y随x的增大而______. |
(6) | 由左至右曲线CG呈下降状态 | 当______时,y随x的增大而___________. |
(7) | 由左至右曲线GK呈____________ | 当______时y随____________. |
(8) | 曲线上的最高点是C(-2,5) | 当x=______时,y有______值,且这个值为____________. |
(9) | 曲线上的最低点是____________ | 当x=______时,y有______值,且这个值为____________. |
(10) | 曲线BCF位于x轴的上方 | 当______时,y______0. |