��Ŀ����
����Ŀ����ѧ���
�����龳��������һ�����⣺̽������![]() ��ͼ�������ʣ�С������ѧϰ�����ľ��飬�Ժ���
��ͼ�������ʣ�С������ѧϰ�����ľ��飬�Ժ���![]() ��ͼ�������ʽ�����̽����
��ͼ�������ʽ�����̽����
��������������С����̽�����̣��벹��������
��1������![]() ���Ա���
���Ա���![]() ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��
��2������![]() ��
��![]() �ļ����Ӧֵ��
�ļ����Ӧֵ��
| �� | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | �� |
| �� |
|
|
| 0 | -1 | 3 | 2 |
|
|
| �� |
��![]() ��ֵ��
��ֵ��
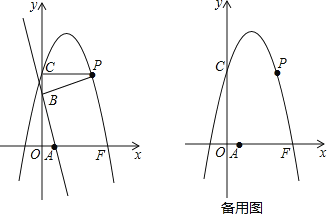
��3����ͼ����ƽ��ֱ������ϵ�У���������ϱ��и��Զ�ӦֵΪ����ĵ㣬��������ĵ㣬�����ú�����ͼ��
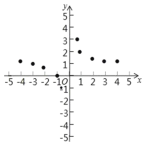
��4����Ϻ�����ͼ��д���ú��������ʣ��������ɣ�
���𰸡���1��![]() ����2��
����2��![]() ��ֵΪ
��ֵΪ![]() ����3������������4��û�����ֵ��û����Сֵ��
����3������������4��û�����ֵ��û����Сֵ��
��������
��1����ͼ����֪x��0��
��2������ͼ����֪��y=-1ʱx=-m����y=-1��x=-m�������ʽ������ã�
��3����������ϵ�еĵ㣬��ƽ����ֱ�����Ӽ��ɣ�
��4���۲�ͼ�ɵó��ú������������ʣ��ú���û�����ֵ��û����Сֵ��
�⣺
��1����������ã�![]() Ϊ����ʵ����
Ϊ����ʵ����
������![]() ���Ա���
���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2����![]() ��
��![]() ���뺯��
���뺯��![]() �еã�
�еã�
![]()
��![]()
![]() ��
��![]() ��ֵΪ
��ֵΪ![]() ��
��
��3����ƽ����������������ͼ������ĵ㣬��ͼ��ʾ
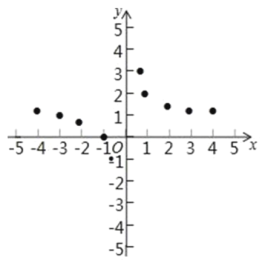
��4���۲캯��ͼ���ָú���û�����ֵ��û����Сֵ��
���ú�����һ�����ʣ�û�����ֵ��û����Сֵ��