题目内容
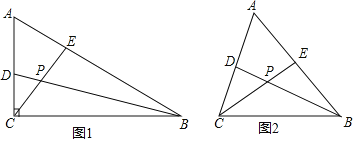
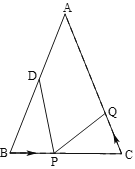
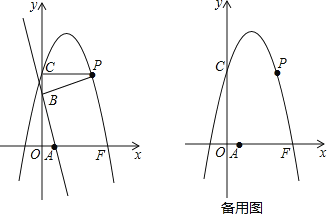
【题目】如图,直线y=﹣3x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c与直线y=c分别交y轴的正半轴于点C和第一象限的点P,连接PB,得△PCB≌△BOA(O为坐标原点).若抛物线与x轴正半轴交点为点F,设M是点C,F间抛物线上的一点(包括端点),其横坐标为m.
(1)直接写出点P的坐标和抛物线的解析式;
(2)当m为何值时,△MAB面积S取得最小值和最大值?请说明理由;
(3)求满足∠MPO=∠POA的点M的坐标.
【答案】(1)点P的坐标为(3,4),抛物线的解析式为y=﹣x2+3x+4;(2)当m=0时,S取最小值,最小值为![]() ;当m=3时,S取最大值,最大值为5.(3)满足∠MPO=∠POA的点M的坐标为(0,4)或(
;当m=3时,S取最大值,最大值为5.(3)满足∠MPO=∠POA的点M的坐标为(0,4)或(![]() ,
,![]() ).
).
【解析】(1)代入y=c可求出点C、P的坐标,利用一次函数图象上点的坐标特征可求出点A、B的坐标,再由△PCB≌△BOA即可得出b、c的值,进而可得出点P的坐标及抛物线的解析式;
(2)利用二次函数图象上点的坐标特征求出点F的坐标,过点M作ME∥y轴,交直线AB于点E,由点M的横坐标可得出点M、E的坐标,进而可得出ME的长度,再利用三角形的面积公式可找出S=﹣![]() (m﹣3)2+5,由m的取值范围结合二次函数的性质即可求出S的最大值及最小值;
(m﹣3)2+5,由m的取值范围结合二次函数的性质即可求出S的最大值及最小值;
(3)分两种情况考虑:①当点M在线段OP上方时,由CP∥x轴利用平行线的性质可得出:当点C、M重合时,∠MPO=∠POA,由此可找出点M的坐标;②当点M在线段OP下方时,在x正半轴取点D,连接DP,使得DO=DP,此时∠DPO=∠POA,设点D的坐标为(n,0),则DO=n,DP=![]() ,由DO=DP可求出n的值,进而可得出点D的坐标,由点P、D的坐标利用待定系数法即可求出直线PD的解析式,再联立直线PD及抛物线的解析式成方程组,通过解方程组求出点M的坐标.综上此题得解.
,由DO=DP可求出n的值,进而可得出点D的坐标,由点P、D的坐标利用待定系数法即可求出直线PD的解析式,再联立直线PD及抛物线的解析式成方程组,通过解方程组求出点M的坐标.综上此题得解.
(1)当y=c时,有c=﹣x2+bx+c,
解得:x1=0,x2=b,
∴点C的坐标为(0,c),点P的坐标为(b,c),
∵直线y=﹣3x+3与x轴、y轴分别交于A、B两点,
∴点A的坐标为(1,0),点B的坐标为(0,3),
∴OB=3,OA=1,BC=c﹣3,CP=b,
∵△PCB≌△BOA,
∴BC=OA,CP=OB,
∴b=3,c=4,
∴点P的坐标为(3,4),抛物线的解析式为y=﹣x2+3x+4;
(2)当y=0时,有﹣x2+3x+4=0,
解得:x1=﹣1,x2=4,
∴点F的坐标为(4,0),
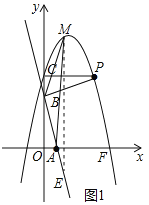
过点M作ME∥y轴,交直线AB于点E,如图1所示,
∵点M的横坐标为m(0≤m≤4),
∴点M的坐标为(m,﹣m2+3m+4),点E的坐标为(m,﹣3m+3),
∴ME=﹣m2+3m+4﹣(﹣3m+3)=﹣m2+6m+1,
∴S=![]() OAME=﹣
OAME=﹣![]() m2+3m+
m2+3m+![]() =﹣
=﹣![]() (m﹣3)2+5,
(m﹣3)2+5,
∵﹣![]() <0,0≤m≤4,
<0,0≤m≤4,
∴当m=0时,S取最小值,最小值为![]() ;当m=3时,S取最大值,最大值为5;
;当m=3时,S取最大值,最大值为5;
(3)①当点M在线段OP上方时,∵CP∥x轴,
∴当点C、M重合时,∠MPO=∠POA,
∴点M的坐标为(0,4);
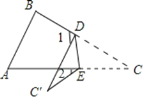
②当点M在线段OP下方时,在x正半轴取点D,连接DP,使得DO=DP,此时∠DPO=∠POA,
设点D的坐标为(n,0),则DO=n,DP=![]() ,
,
∴n2=(n﹣3)2+16,
解得:n=![]() ,
,
∴点D的坐标为(![]() ,0),
,0),
设直线PD的解析式为y=kx+a(k≠0),
将P(3,4)、D(![]() ,0)代入y=kx+a,
,0)代入y=kx+a,
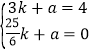 ,解得:
,解得: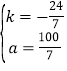 ,
,
∴直线PD的解析式为y=﹣![]() x+
x+![]() ,
,
联立直线PD及抛物线的解析式成方程组,得: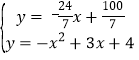 ,
,
解得:![]() ,
,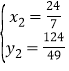 .
.
∴点M的坐标为(![]() ,
,![]() ).
).
综上所述:满足∠MPO=∠POA的点M的坐标为(0,4)或(![]() ,
,![]() ).
).
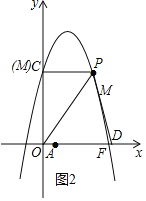

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】根据下面的研究弹簧长度与所挂物体重量关系的实验表格,不挂物体时,弹簧原长_____cm;当所挂物体重量为3.5kg时,弹簧比原来伸长_____cm.
所挂物体重量x(kg) | 1 | 3 | 4 | 5 |
弹簧长度y(cm) | 10 | 14 | 16 | 18 |