题目内容
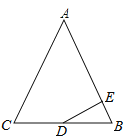
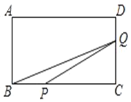
【题目】如图1,抛物线y=﹣![]() x2+bx+c与x轴交于点A(4,0),与y轴交于点B(0,4),在x轴上有一动点D9(m,0)(0<m<4),过点D作x轴的垂线交直线AB于点C,交抛物线于点E,
x2+bx+c与x轴交于点A(4,0),与y轴交于点B(0,4),在x轴上有一动点D9(m,0)(0<m<4),过点D作x轴的垂线交直线AB于点C,交抛物线于点E,
(1)直接写出抛物线和直线AB的函数表达式.
(2)当点C是DE的中点时,求出m的值,并判定四边形ODEB的形状(不要求证明).
(3)在(2)的条件下,将线段OD绕点O逆时针旋转得到OD′,旋转角为α(0°<a<90°),连接D′A、D′B,求D′A+![]() D′B的最小值.
D′B的最小值.

【答案】(1)y=﹣![]() ;y=﹣x+4;(2)m=2,四边形ODEB为矩形;(3)
;y=﹣x+4;(2)m=2,四边形ODEB为矩形;(3)![]()
【解析】
(1)利用待定系数法求出抛物线解析式和直线AB的解析式即可;
(2)可得E(m,![]() ),C(m,﹣m+4).表示出EC的长,根据EC=CD可得出关于m的方程,解方程求出m的值即可;
),C(m,﹣m+4).表示出EC的长,根据EC=CD可得出关于m的方程,解方程求出m的值即可;
(3)在y轴上取一点M′使得OM′=1,连接AM′,在AM′上取一点D′使得OD′=OD.证明△M′OD′∽△D′OB,即可求解.
(1)将点B、A的坐标代入抛物线y=﹣![]() x2+bx+c得,
x2+bx+c得,
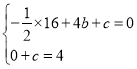 ,
,
解得:![]() ,
,
∴抛物线的函数表达式为y=﹣![]() .
.
设直线AB的解析式为y=kx+b,
∴![]() ,
,
解得:![]() ,
,
∴直线AB的解析式为y=﹣x+4;
(2)∵过点D(m,0)(0<m<4)作x轴的垂线交直线AB于点C,交抛物线于点E,
∴E(m,![]() ),C(m,﹣m+4).
),C(m,﹣m+4).
∴EC=![]() =
=![]() .
.
∵点C是DE的中点,
∴![]() .
.
解得:m=2,m=4(舍去).
∴ED=OB=4,
∴四边形ODEB为矩形.
(3)如图,由(2)可知D(2,0),在y轴上 取一点M′使得OM′=1,连接AM′,在AM′上取一点D′使得OD′=OD.
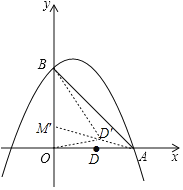
∵OD′=2,OM′OB=1×4=4,
∴OD′2=OM′OB,
∴![]() ,
,
∵∠BOD′=∠M′OD′,
∴△M′OD′∽△D′OB,
∴![]() .
.
∴![]() .
.
∴D′A+![]() D′B=D′A+M′D′=AM′,此时D′A+
D′B=D′A+M′D′=AM′,此时D′A+![]() D′B最小(两点间线段最短,A、M′、D′共线时),
D′B最小(两点间线段最短,A、M′、D′共线时),
∴D′A+![]() D′B的最小值=AM′=
D′B的最小值=AM′=![]() =
=![]() .
.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】数学活动:
问题情境:有这样一个问题:探究函数![]() 的图象与性质,小明根据学习函数的经验,对函数
的图象与性质,小明根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
问题解决:下面是小明的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)表是![]() 与
与![]() 的几组对应值.
的几组对应值.
| … | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | … |
| … |
|
|
| 0 | -1 | 3 | 2 |
|
|
| … |
求![]() 的值;
的值;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象.
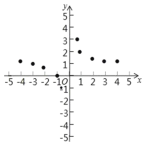
(4)结合函数的图象,写出该函数的性质(两条即可)
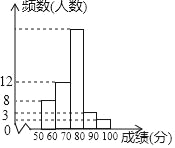
【题目】(7分)某中学1000名学生参加了”环保知识竞赛“,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x≤100 | b | c |
合计 | ■ | 1 |
(1)写出a,b,c的值;
(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
(3)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取两名同学参加环保知识宣传活动,求所抽取的2名同学来自同一组的概率.