题目内容
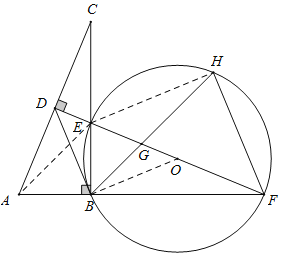
【题目】(本小题满分10分)如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且BF=BC.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交于点H,连接BD、FH.
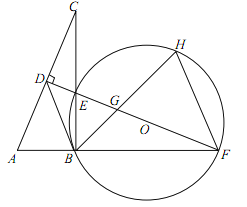
(1)求证:△ABC≌△EBF;
(2)试判断BD与⊙O的位置关系,并说明理由;
(3)若AB=1,求HGHB的值.
【答案】(1)证明见试题解析;(2)相切,理由见试题解析;(3)![]() .
.
【解析】
试题(1)由∠ABC=90°和FD⊥AC,得到∠ABF=∠EBF,由∠DEC=∠BEF,得到∠DCE=∠EFB,从而得到△ABC≌△EBF(ASA);
(2)BD与⊙O相切.连接OB,只需证明∠DBE+∠OBE=90°,即可得到OB⊥BD,从而有BD与⊙O相切;
(3)连接EA,EH,由DF为线段AC的垂直平分线,得到AE=CE,由△ABC≌△EBF,得到AB=BE=1,进而得到CE=AE=![]() ,故
,故![]() ,即可得出结论
,即可得出结论![]() ,
,
又因为BH为角平分线,易证△EHF为等腰直角三角形,故![]() ,得到
,得到![]() ,再由△GHF∽△FHB,得到
,再由△GHF∽△FHB,得到![]() .
.
试题解析:(1)∵∠ABC=90°,∴∠CBF=90°,∵FD⊥AC,∴∠CDE=90°,∴∠ABF=∠EBF,∵∠DEC=∠BEF,∴∠DCE=∠EFB,∵BC=BF,∴△ABC≌△EBF(ASA);
(2)BD与⊙O相切.理由:连接OB,∵DF是AC的垂直平分线,∴AD=DC,∴BD=CD,∴∠DCE=∠DBE,∵OB=OF,∴∠OBF=∠OFB,∵∠DCE=∠EFB,∴∠DBE=∠OBF,∵∠OBF+∠OBE=90°,∴∠DBE+∠OBE=90°,∴OB⊥BD,∴BD与⊙O相切;
(3)连接EA,EH,∵DF为线段AC的垂直平分线,∴AE=CE,∵△ABC≌△EBF,∴AB=BE=1,∴CE=AE=![]() ,∴
,∴![]() ,∴
,∴![]() ,又∵BH为角平分线,∴∠EBH=∠EFH=45°,∴∠HEF=∠HBF=45°,∠HFG=∠EBG=45°,∴△EHF为等腰直角三角形,∴
,又∵BH为角平分线,∴∠EBH=∠EFH=45°,∴∠HEF=∠HBF=45°,∠HFG=∠EBG=45°,∴△EHF为等腰直角三角形,∴![]() ,∴
,∴![]() ,∵∠HFG=∠FBG=45°,∠GHF=∠GHF,∴△GHF∽△FHB,∴
,∵∠HFG=∠FBG=45°,∠GHF=∠GHF,∴△GHF∽△FHB,∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.

【题目】某商店销售一种商品,经市场调査发现,该商品的周销售量y(件)是售价x(元/件)的一次函数.其售价、周销售量、周销售利润w(元)的三组对应值如表:
售价x(元/件) | 50 | 60 | 80 |
周销售量y(件) | 100 | 80 | 40 |
周销售利润w(元) | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价﹣进价)
(1)求y关于x的函数解析式_____;
(2)当售价是_____元/件时,周销售利润最大.
【题目】数学活动:
问题情境:有这样一个问题:探究函数![]() 的图象与性质,小明根据学习函数的经验,对函数
的图象与性质,小明根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
问题解决:下面是小明的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)表是![]() 与
与![]() 的几组对应值.
的几组对应值.
| … | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | … |
| … |
|
|
| 0 | -1 | 3 | 2 |
|
|
| … |
求![]() 的值;
的值;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象.
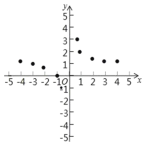
(4)结合函数的图象,写出该函数的性质(两条即可)
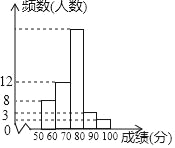
【题目】(7分)某中学1000名学生参加了”环保知识竞赛“,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x≤100 | b | c |
合计 | ■ | 1 |
(1)写出a,b,c的值;
(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
(3)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取两名同学参加环保知识宣传活动,求所抽取的2名同学来自同一组的概率.