Question

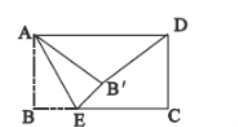
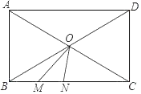
【题目】如图，O为矩形ABCD对角线AC，BD的交点，AB＝9，AD＝18，M，N是直线BC上的动点，且MN＝3，则OM+ON最小值＝___．

Answer 1

【答案】3．

【解析】

通过作图得到平行四边形MNQP，由平行四边形MNQP的性质得到OM+ON＝QN+ON，从而得到当O，N，Q在同一直线上时，OM+ON最小，即OM+ON＝OQ；由轴对称的性质得到OP长度，最后根据勾股定理得到OQ的值，从而得到答案.

如图所示，作点O关于BC的对称点P，连接PM，将MP沿着MN的方向平移MN长的距离，得到NQ，连接PQ，

则四边形MNQP是平行四边形，

∴MN＝PQ＝3，PM＝NQ＝MO，

∴OM+ON＝QN+ON，

当O，N，Q在同一直线上时，OM+ON的最小值等于OQ长，

连接PO，交BC于E，

由轴对称的性质，可得BC垂直平分OP，

又∵矩形ABCD中，OB＝OC，

∴E是BC的中点，

∴OE是△ABC的中位线，

∴OE＝AB＝4.5，

∴OP＝2×4.5＝9，

又∵PQ∥MN，

∴PQ⊥OP，

∴Rt△OPQ中，OQ＝＝＝3，

∴OM+ON的最小值是3，

故答案为：3．